PeakLab v1 Documentation Contents AIST Software Home AIST Software Support
Giddings
The Giddings Model
a0 = Area
a1 = Center (as mean of asymmetric peak)
a2 = Kinetic Width (as time constant)
Built in model: Giddings
User-defined peaks and view functions: Giddings(x,a0,a1,a2)
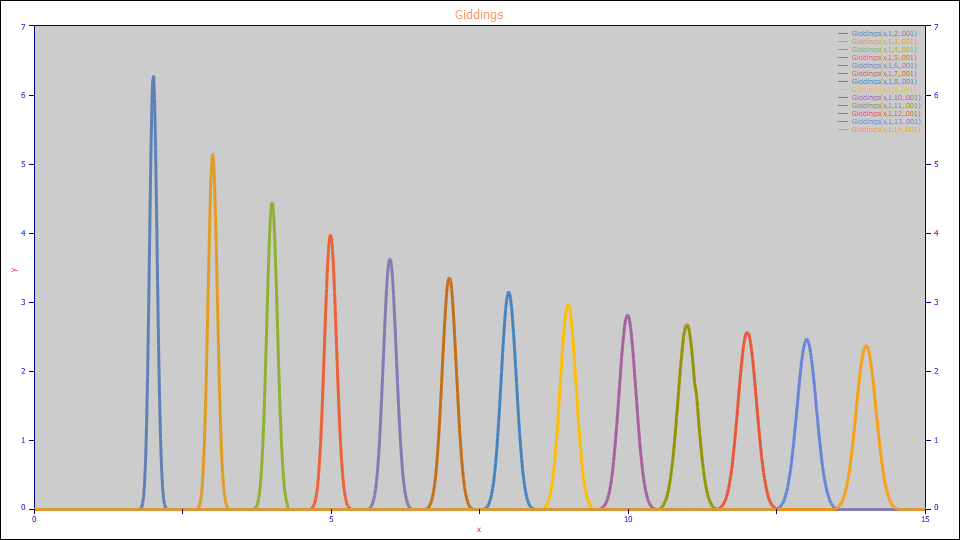
The Giddings model is a peak formed by first order kinetics. In the above plot, all of the peaks have equal area and the same a2 kinetic time constant. The peaks broaden and are attenuated in amplitude with increasing retention time. When fitting a Giddings, NLC, or GenNLC model, and assuming constant kinetics, peaks are expected to widen with retention time irrespective of the magnitude of any a3 distortion.
The Giddings equation was derived by J. C. Giddings (Dynamics of Chromatography, Part I, Marcel Decker, New York, 1965). The equation provides a theoretical description for chromatographic peaks obtained under linear conditions (no column overload), where the kinetic rates of adsorption and desorption are the primary source of band broadening. Diffusion, dispersion, and extracolumn effects are assumed negligible. Where interphase mass transfer can be modeled with first order “rate constants” of mass transfer, the equation is also valid. The equation models only kinetic effects, and can fit only slightly tailed peaks.
Assuming the data has been properly transformed, the a1 “center” parameter is the true thermodynamic capacity factor k’. The time transformation can be carried out as follows: X=X/t0 -1, where t0 is the dead time of the column. The a1 parameter is also the first statistical moment, or centroid.
Under certain unusual conditions corresponding with large a2, a peak appears to lose mass. This is the “split peak” condition where a fraction elutes at the column void volume (t/t0 =1), and a fraction is retained. It arises when the kinetics of adsorption and desorption are so slow that a solute molecule has a finite probability of traversing the column without adsorbing even once. The split peak effect is occasionally observed in affinity chromatography.
The a2 width parameter has physical significance in that its inverse is actually a dimensionless rate constant:
where kd is the solute desorption constant, and t0 is the dead time of the column.
As a practical matter, the kinetic constants derived by fitting this model will reflect lumped contributions from effects other than chemical desorption such as slow interphase mass transfer, axial dispersion, and extracolumn effects. As such, it is generally unwise to regard rate constants derived in this way as representing only one chemical process.
Giddings Considerations
The Giddings equation represents the limiting case for the NLC function for the infinitely dilute case of zero overload (NLC a3 =0), and thus the Giddings is the zero-distortion density (ZDD) in the NLC model.
Note that the Giddings model has no chromatographic distortion or a3 asymmetry term. In practical terms, the Giddings model is a component of a chromatographic model as not a model useful for fitting. You should use the NLC, or one of the GenNLC models to fit a Giddings kinetic width. These will reduce to a Giddings if there is no chromatographic distortion
When the Giddings is fitted as a separate model, the function is fitted precisely as above, using the modified Bessel function. The Giddings(x,a0,a1,a2) is the view function and user-defined peak function for this full precision Giddings density. The TFn(u,v) can be used to get the full precision modified Bessel function integral of the Giddings (as used in the pure NLC).
In the Fast NLC, the Giddings and its cumulatives are used in computationally fast approximations. If you are creating generalized user-defined peaks incorporating the Giddings model and especially its cumulatives, you will probably want to use the Gidx(x,a0,a1,a2), Gidx_C(x,a0,a1,a2), and the Gidx_CR(x,a0,a1,a2) approximation for the density, cumulative, and reverse cumulative.


 |