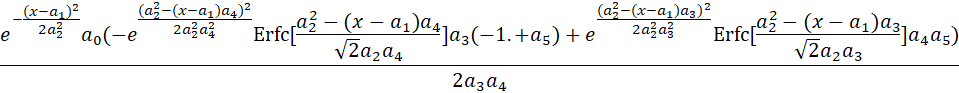
PeakLab v1 Documentation Contents AIST Software Home AIST Software Support
E2AMG
E2AMG Gaussian Convolved with Sum of Fast and Slow Exponential, Area Weighted
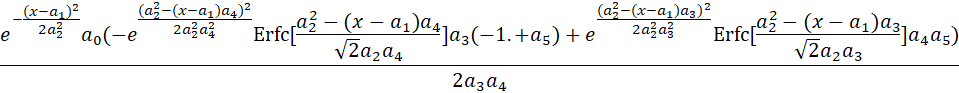
a0 = Area
a1 = Center (as mean of Gaussian peak that is convolved by the sum of half-Gaussian and exponential)
a2 = Width (SD of the Gaussian peak that is convolved by the sum of half-Gaussian and exponential)
a3 =The fast first order kinetic or exponential decay width (time constant) in the convolution (must be positive, right-sided convolution)
a4 =The slow first order kinetic or exponential decay width (time constant) in the convolution (must be positive, right-sided convolution)
a5 = The area fraction of the fast component
Built in model: E2AMG
User-defined peaks and view functions: E2AMG(x,a0,a1,a2,a3,a4,a5)
The E2AMG model is the convolution of a Gaussian and <e2> IRF (area weighted sum of two first order exponential kinetic decays). The E2AMG can also be written as the Gauss<e2> convolution. Unlike the generalized chromatographic models that address nonlinear tailing and fronting and higher moment non-ideality, the E2AMG convolution integral has a closed form, easily computed, solution as shown above.
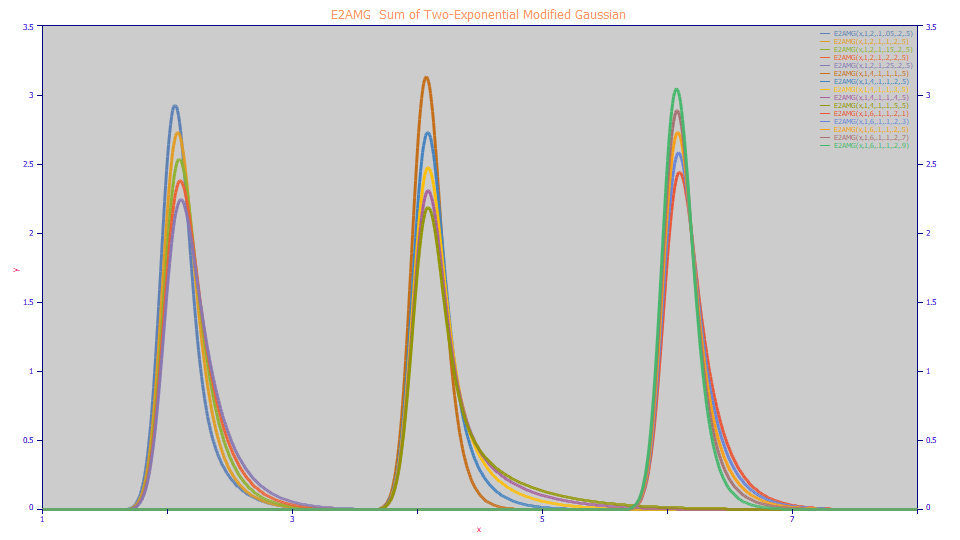
In the first series of peaks the fast kinetic component's tau or time constant is varied. In the second series, the slow exponential component's tau is varied. The slower kinetic component will produce the greater attenuation of the peak amplitude and it will produce most of the right-side tailing. The third series varies the area fraction of the two components, each held constant in their widths.
Two-Component IRF with Closed-Form Solution
Chromatographic IRFs tend to have a slow component, fitted by this exponential, and a fast component which can be fit with a narrow width half-Gaussian or fast kinetic delay. The E2AMG is important since it offers a Gaussian peak with a two-component IRF in a closed-form solution.
Theoretical Foundations for E2AMG Model
This is the closed-form model to which the once-generalized GenHVL[Z]<e2> simplifies if the a3 chromatographic distortion in the GenHVL[Z]<e2> is effectively zero (the chromatography is purely in the linear regime of concentration) and if the a4 third-moment asymmetry in the GenHVL[Z]<e2> is also effectively zero (a symmetric peak is observed in the separation independent of the IRF).
The twice-generalized GenHVL[Y]<e2> similarly simplifies to the E2AMG if the chromatographic distortion is zero, the asymmetry is zero, and the GenHVL[Y]<e2> model's fourth moment power of decay is 2.0, a Gaussian.
The GenNorm<e2>simplifies to the E2AMG if the asymmetry in the GenNorm<e2> is effectively zero (a symmetric peak is observed in the separation).
Similarly, the GenError<e2> simplifies to the E2AMG if the asymmetry in the GenError<e2> is zero, and the GenError<e2> model's fourth moment power of decay is 2.0, a Gaussian.
Right-Skewed Shapes Only
In PeakLab, the E2AMG is treated as the Gauss<e2> convolution model where the a3-a5 'e2' parameters are the IRF parameters.
The more complex, non-closed form, theoretical chromatographic models address the concentration-dependent non-linear tailing and fronting, as well as higher moment non idealities in the separation that introduce both left and right skewed shapes. Since there are far more effective models to manage fronted and left-skewed peak shapes, the E2AMG is constrained to functioning as a Gauss<e2> model that treats the two components of the convolution as instrumental distortions adding right skew to the peak shape.
We thus treat the E2AMG as a theoretical model for chromatography where the core column peak is Gaussian, and the IRF consists of the sum of two kinetic components. This means the E2AMG can only fit right-skewed shapes.
By contrast, the EMG and GMG models in PeakLab were historically used as empirical models for both left and right skewed shapes, and those models will fit left skewed shapes using a negative time constant or negative SD. The E2AMG model, as implemented in PeakLab, cannot be used a general empirical model that manages left skewed peaks.
Chiral Separations
The two main requirements to fit the E2AMG are often met in chiral separations. They can be fully in the linear range of concentration, isocratic, and chiral columns and separations can produce close to symmetric Gaussian peaks if the IRF is excluded.
 |