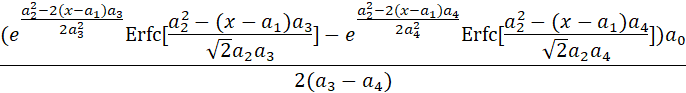
PeakLab v1 Documentation Contents AIST Software Home AIST Software Support
E2xMG
E2xMG (EMG Ä Exponential, Gauss Ä Exponential Ä Exponential)
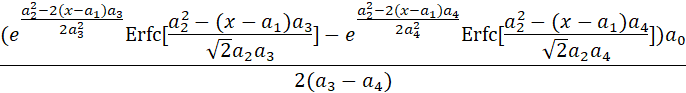
a0 = Area
a1 = Center (as mean of Gaussian peak that is successively convolved by two different exponentials)
a2 = Width (SD of the Gaussian peak that is is successively convolved by two different exponentials)
a3 =The first exponential decay width (time constant) in the convolution sequence
a4 = The second exponential decay width (time constant) in the convolution sequence
Built in model: E2xMG
User-defined peaks and view functions: E2xMG(x,a0,a1,a2,a3,a4)
The E2xMG model is the convolution of a Gaussian and <e2x> IRF (convolution of two exponentials). The E2xMG can also be written as the Gauss<e2x> convolution or Guess Ä Exp Ä Exp, or as EMG Ä Exp. Unlike the generalized chromatographic models that address nonlinear tailing and fronting and higher moment non-ideality, the E2xMG convolution integral has a closed form, easily computed, solution as shown above. Unlike the E2AMG, the two convolution components are deemed to sequential instead of simultaneous, and as such there is no area term.
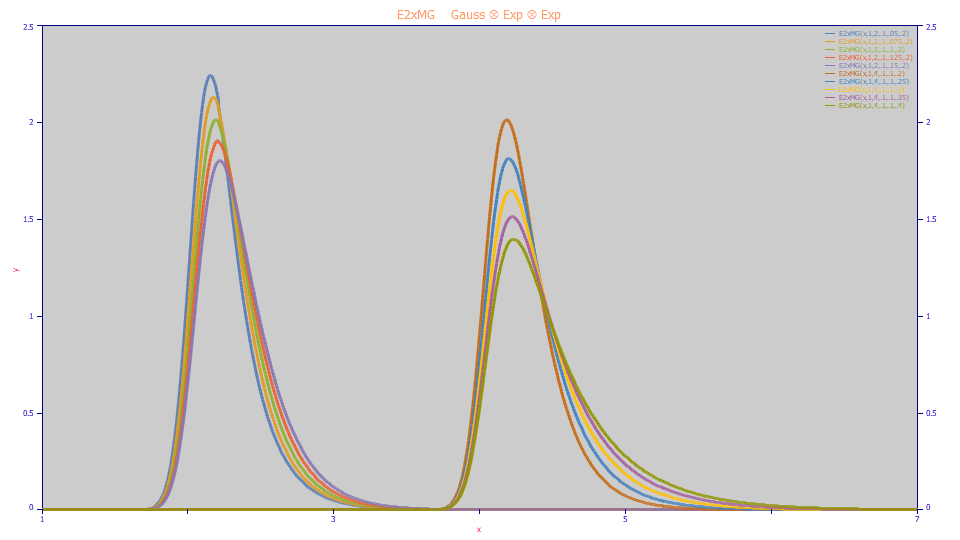
In the first series of peaks the faster kinetic component's tau or time constant is varied. In the second series, the slower exponential component's tau is varied. It is what one would expect from a faster and slower component. The slower kinetic component will produce the greater attenuation of the peak amplitude and it will produce more of the right-side tailing.
Because convolution is commutative, the order does not matter. One can convolve the Gaussian and exponential to produce the EMG and then convolve the EMG with an exponential to get the E2xMG; or the two kinetic IRF components can be convolved and that resultant IRF can then be convolved the with Gaussian. The result is the same; the convolutions can come in any order.
Experimental Model
This is a PeakLab experimental model that was designed to see if pre-column delay Ä column peak Ä post-column delay, or column peak Ä post-column/pre-detector delay Ä detector delay, could be separated and quantified in this type of kinetic modeling. At the time this is being written, the utility of this model is unknown. We do know fitting this model is often difficult if the two exponentials start to approach the same time constant. Axial dispersion will also be present in any LC separation, and we do not believe it will be well modeled by the exponential of first order kinetics.
For this type of experimental study, we also refer you to the Gauss<gex>, HVL<gex>, and GenHVL<gex> models whose IRF is a convolution of an exponential first order kinetic decay and a half-Gaussian probabilisitic delay. Note that none of the <gex> models have closed form solutions, and must be fit with PeakLab's advanced Fourier methods. The same is true of the Gauss<g2x>, HVL<g2x>, and GenHVL<g2x> models where the IRF is a convolution of two half-Gaussians.
It is possible that these <e2x> and <gex> models, where the IRF is itself a convolution, are more likely to apply to separations where the detector indirectly signals the analyte by a rate-dependent kinetic process, such as flame ionization as opposed to a direct conductivity or spectral signaling.
 |