PeakLab v1 Documentation Contents AIST Software Home AIST Software Support
GLM Prediction
The Prediction button in the GLM Review opens a file selection window where you must specify a file containing the data matrix that will be used to evaluate the prediction accuracy of model. The prediction data will usually be out-of-sample data (that which was nowhere used in the design model), but it can be any data matrix, including the data that was used for the original modeling.
You can only access the Prediction procedure from the GLM Review. This is opened at the conclusion of any current fit, or in loading any saved fit (these are binary files with BIN extensions).
The prediction data's X-predictor names or WL/Wn values must match those in the design data. The prediction data's Y value column must be specified if its name doesn't match with any of the column names/identifiers in the design data matrix file. If the Y data does not exist, you must check No Y data is available.
Once the prediction data has been loaded, a window is opened containing Prediction statistics and the sample by sample prediction information for the model currently selected and graphed in the GLM Review. This will be an RTF (rich text format) window where individual content can be highlighted and copied, provided the size of the predicted data consists of less less than 2048 data samples/spectra. For larger sets, a much faster display procedure is used for accommodating the display of up to the program's N=50,000 built-in data limit.
The purpose of the GLM Prediction procedure is to evaluate the predictive accuracy of individual fitted models, and possibly to see the prediction statistics of the original design data when possible data outliers are omitted post-fitting by one or both of two different methods.
Original Fit Prediction Statistics
Since the fit statistics used for model selection are based on a prediction method applied to the original fitting procedure, this is shown first in the summary:
Prediction Statistics - from Original Fit - Leave One Out
301 Observations
r2 SE F-stat AICc BIC MDL DOF
0.9620772 0.6234001 666.52260 584.73838 631.66252 666.70036 289
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.3161475 0.4369066 0.4212597 0.3587225 0.4009056 0.3988211 0.5987931
Quintile Lower Upper
First 0.0600000 2.1580538
Second 2.1580538 2.9349223
Third 2.9349223 3.5834400
Fourth 3.5834400 6.1752371
Fifth 6.1752371 14.852395
This will be same prediction information that is shown in the GLM Numeric Summary. This information will pertain to the original data matrix used at the time of fitting, and not to the prediction data loaded in the GLM Prediction procedure. For detailed information of the Leave One Out or Random Sampling prediction estimates used in the fitting procedure, please refer to the GLM Numeric topic.
The original prediction statistics are useful for comparing the different prediction methodologies available at the time of fitting with that which is seen with the data imported for prediction, typically blind out-of-sample data.
In-Sample and Out-of-Sample Data
In general, one would expect the blind data to fare more poorly with respect to prediction accuracy. One reason would be the possibility that the blind out-of-sample data consists of spectra which push the bracketing of the modeling problem beyond that which was addressed in the design fitting. Another reason is that outlier detection is often applied to the original design model data-it is often cleaned since the fitting process helps identify outliers, especially those originating with human error. In a prediction, without fitting, it is harder to declare a given data sample as one containing such an error. As such, the model data may well yield lower prediction errors, irrespective of the type of prediction error algorithm used.
You must be careful in using later samples in time to represent out-of-sample (blind prediction) data and earlier samples in time to represent in-sample (design model) data. Across time, much within a chromatography-spectroscopy modeling system can change. Columns, light sources, and other instrument components impacting the IRF (instrument response function) peak broadening, can subtly change or age, laboratory procedures may inadvertently change, and the analysis environments may not be constant. You would expect to have to redo all predictive models if, for example, the spectroscopy were to be shifted to a next generation instrument, especially if the sources, optics, and detectors produced spectral peaks of narrower widths.
One way to gauge the validity of the specific frequencies or wavelengths used in a predictive model is to use a rigorous method for in-sample and out-of-sample data. You can use the Modify GLM Data Matrix menu's Generate Random Sampling GLM Data Matrices... item to generate random samples for estimation and prediction across all available data. This will force the fitted models to adapt to any changes which occur across time. A half-dozen design/prediction random pairs of data matrices should sufficiently answer this question of principal frequencies.
Prediction Statistics from Prediction-Specific Data Matrix
If the prediction data contains a known Y-value column, this Prediction Statistics section based on the imported prediction data will be present in the summary shown in this window.
No Inactive Data in GLM Review Graph
If the Mark Inactive Outside Prediction Interval option has not been used in the GLM Review graph's right click menu, the prediction statistics in the first section will reflect all of the data within the imported prediction data matrix. None will be inactive or excluded.
Prediction Statistics - from Prediction Data
154 Observations
r2 SE F-stat AICc BIC MDL DOF
0.6875128 1.0548136 53.903221 463.29821 486.60073 496.49182 147
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.5490547
0.7477224
0.8040008
0.7036582
0.4773340
0.8148846
1.5695040
If the Prediction summary's Outliers option is enabled, there will be a second section showing the different prediction statistics arising from the omission of these specific data samples. This is what is shown for the above prediction statistics when all prediction observations are required to be within 2 SE's (computed using the sum of squared prediction errors as the SSE in the SE formula):
Prediction Statistics - 11 Outliers Removed
143 Observations
r2 SE F-stat AICc BIC MDL DOF
0.7520573 0.7580341 68.752289 336.48421 359.11234 371.41185 136
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.4615657
0.6007199
0.8040008
0.6280731
0.4773340
0.6552422
0.8849382
The prediction statistics are also covered in detail in the GLM Numeric topic. In essence, the sum of squared prediction errors are used as the SSE in a conventional goodness of fit analysis, even though no fit of any kind has occurred with the prediction data. Still, the goodness of fit values are interesting for comparison, even though no minimization or modeling has occurred. Typically, you will probably find the average and median prediction errors to be more useful.
In this example, the prediction data matrix, as is, produces median errors about 73% higher, and average errors about 71% higher than those seen with the cleaned design matrix data. If 11 of the 154 data sets are removed in this +/- 2SE exclusion, the median prediction errors are about 46% higher on the out-of-sample data, and the average errors are about 37% higher. This example is intentional and illustrates the danger of having all out-of-sample data subsequent in time to the in-sample data.
If the the Modify GLM Data Matrix menu's Generate Random Sampling GLM Data Matrices... item is used to generate a different random in-sample and out-of-sample set of the same sizes:
Prediction Statistics - from Original Fit - Leave One Out
301 Observations
r2 SE F-stat AICc BIC MDL DOF
0.9324721 0.6730456 331.40888 632.02321 682.45422 709.55188 288
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.3537915 0.4725559 0.4465846 0.3246582 0.3903833 0.4333004 0.7475568
Prediction Statistics - from Prediction Data
154 Observations
r2 SE F-stat AICc BIC MDL DOF
0.9368390 0.8204240 174.28255 393.50929 433.00505 459.48887 141
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.3796138 0.5495779 0.4466843 0.5158296 0.4529093 0.3803100 0.8863866
This is more typical of what you want to see in a predictive model. The random out-of-sample set has a median error 7% higher and an average error 16% higher than the random in-sample data.
Inactive Data in GLM Review Graph
If the Mark Inactive Outside Prediction Interval option has been used in the GLM Review graph's right click menu, the prediction statistics in the first section will reflect only the data that falls within the prediction interval set in the Graph's toolbar for the intervals. Please note that the graph's prediction interval is not the prediction interval of the multivariate fit, but rather that of the linear fit between the known and estimated Y values.
![]() Use the Confidence
Intervals button in the graph toolbar to change the prediction interval confidence.
Use the Confidence
Intervals button in the graph toolbar to change the prediction interval confidence.
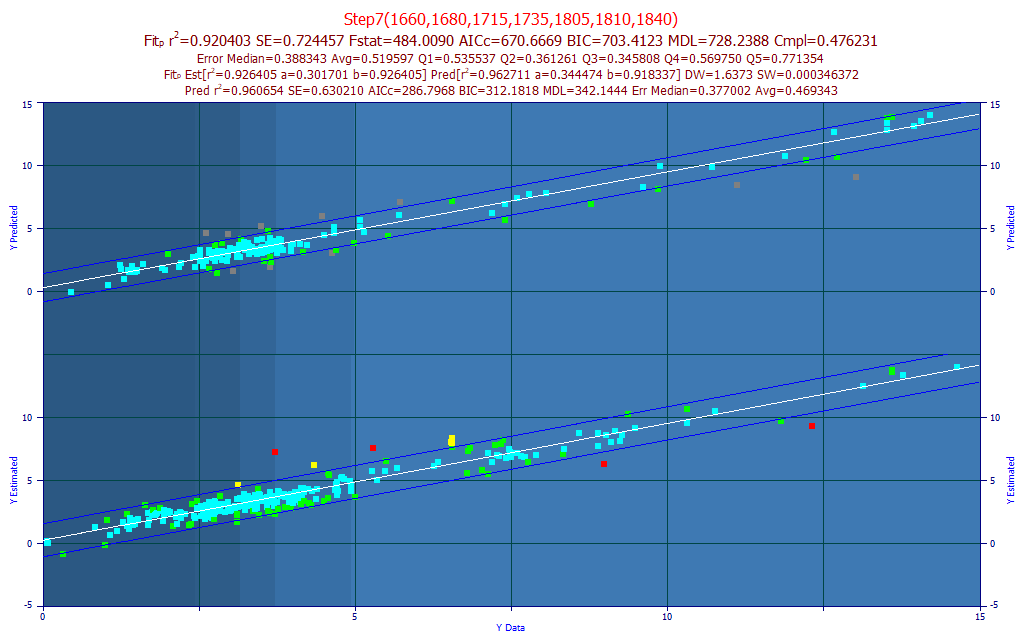
In the above plot, the graph's prediction intervals were set at a 95% confidence and the Mark Inactive Outside Prediction Interval right-click menu option was selected. Note that 10 of the 154 observations were marked as inactive. These points, corresponding to individual data sets or spectra, are grayed out in the graph.
Prediction Statistics - from Prediction Data (10 Inactive)
144 Observations
r2 SE F-stat AICc BIC MDL DOF
0.9606543 0.6302105 474.36294 286.79676 312.18180 342.14441 136
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.3770015 0.4693426 0.3984990 0.4075996 0.4225930 0.4122854 0.6957282
Prediction Statistics - 15 Outliers Removed
139 Observations
r2 SE F-stat AICc BIC MDL DOF
0.9667372 0.5465539 543.90485 237.67480 262.68972 294.14196 131
Median Err Avg Err Avg Err Q1 Avg Err Q2 Avg Err Q3 Avg Err Q4 Avg Err Q5
0.3717074 0.4243321 0.3984990 0.4075996 0.4225930 0.4122854 0.4822063
When this is done, the Inactive count will be displayed in the first section. The second section's Outliers Removed will automatically include the 10 inactive data sets carried over from the main graph. Here 5 additional data sets were omitted from the Outliers menu's Flag Standardized Residuals Outliers, this with Multiples of SE set to Outside of 2 SE.
Prediction Data
Prediction Data
144 Observations
Data Yobserved Ypredict Residual ResStnd * ID
1 2.7900000 3.1221742 -0.332174 -0.460064 1 "S003(2.79-10.13-10.34)"
2 1.3600000 1.7913203 -0.431320 -0.597382 2 "S011(1.36-4.73-4.73)"
3 2.4700000 2.9298198 -0.459820 -0.636854 3 "S013(2.47-8.62-8.76)"
4 2.5100000 3.3401414 -0.830141 -1.149752 4 "S014(2.51-9.39-9.62)"
5 3.2100000 3.9868963 -0.776896 -1.076007 5 "S023(3.21-10.37-10.37)"
6 2.0000000 3.0511478 -1.051148 -1.455848 6 "S025(2.-6.21-6.21)"
7 8.7600000 7.0338532 1.7261468 2.3907266 7 "S026(8.76-34.82-34.69)"
8 2.4700000 2.8929090 -0.422909 -0.585732 8 "S029(2.47-7.68-7.68)"
9 3.2400000 3.4407028 -0.200703 -0.277975 9 "S030(3.24-10.88-10.88)"
10 3.0900000 3.2110560 -0.121056 -0.167664 10 "S037(3.09-12.3-12.3)"
11 1.6000000 2.2359525 -0.635953 -0.880799 11 "S049(1.6-5.68-5.68)"
12 1.2400000 1.8985859 -0.658586 -0.912147 12 "S052(1.24-3.87-3.87)"
13 3.4800000 5.2591599 -1.779160 -2.464150 * 13 "S056(3.48-10.42-10.42)"
14 2.5100000 2.9240611 -0.414061 -0.573478 14 "S057(2.51-8.89-8.87)"
15 1.4100000 2.0648261 -0.654826 -0.906939 15 "S058(1.41-4.35-4.35)"
16 2.9500000 4.6345460 -1.684546 -2.333109 * 16 "S063(2.95-9.33-9.33)"
17 2.7800000 1.5674744 1.2125256 1.6793573 17 "S068(2.78-9.62-9.62)"
18 1.2900000 1.0631147 0.2268853 0.3142379 18 "S069(1.29-4.45-4.44)"
This is the data set prediction summary when there is a known Y value column in the prediction data. The standardized residuals will be highlighted if the removal occurred solely from the Outlier SE setting in the procedure. The data set will be grayed if it was omitted as a consequence of using the Mark Inactive Outside Prediction Interval right click menu option in the GLM Review graph.
File Menu
The Save Summary As... option will save the information in the GLM Prediction Summary to a comma separated value CSV file, a tab-separated PRN file, or a space-formatted TXT file. In addition to these three ASCII formats, you can also save the file as a rich text format RTF file that preserves all formatting and can be imported into programs such as MS Word.
The Save Summary and X-Predictor Data As... option will save the information in the GLM Prediction Summary as well as the raw Y and X-data in the prediction data matrix to a comma separated value CSV file. This option extracts only the specific X-predictors used in the current model and writes an Excel importable file with the parameters and a text string containing the formula for the model in a cell to the far right of the sheet. It will look something like $P$1+SUMPRODUCT($H2:$N2,$Q$1:$W$1). You will need to enter this cell and place an = sign at the start to make it a formula. You can then copy this formula to all of the rows, evaluating all of the prediction data.
The Stream Summary to MS Word or RTF file... option will open a stream target if one is not open, and it will stream the content of the summary into MS Word directly or into an RTF file. If you do not have MS Word on your machine, only the RTF option will be available.
The Save Data w/Inactive Observations Removed will create a comma separated value CSV data matrix file with the currently omitted observations absent.
Use the Printer Setup item to select and configure the printer you wish to use to print the summary. Use the Print item in the File menu to initiate the printing.
Edit Menu
Use the Copy option to place the summary on the clipboard. Both RTF and text formats will be copied.
Use the Copy w/Formatting option to use MS Word to place the formatted summary on the clipboard. No text format copy will exist.
The ASCII Editor option will convert the summary to ASCII text and open an editor. You can use the ASCII Editor to convert between different ASCII delimiters.
Language Code Options
The Copy Prediction Evaluations for Maple will place Maple text on the clipboard. When pasted into Maple, this will replicate the computations of the predictions within the Maple environment. This does include Maple evaluation code for the current model.
Parms:=[3.16980717507832,-1893.54703371262,3276.20797708183,939.876837895965,-3013.815820557,3347.26594466882,-1641.06044939735,-1016.84920399738]:
WL:=[1660,1680,1715,1735,1805,1810,1840]:
mSpec:=[[1,0.61013037,0.610615253,0.613445401,0.613648176,0.610915303,0.610187292,0.605716109],
[1,0.588049471,0.588013291,0.5908373,0.591266096,0.588798761,0.588066161,0.583659887],
...
pred :=array(1..154):
for i from 1 to 154 do
p := 0: for j from 1 to 8 do p := p + mSpec[i,j]*Parms[j]: od:
pred[i] := p:
od:
print(pred);
The Copy Prediction Evaluations for Mathematica will place Mathematica text on the clipboard. When pasted into Mathematica, this will replicate the computations of the predictions within the Mathematica environment. This does include Mathematica evaluation code for the current model.
Parms:={3.16980717507832,-1893.54703371262,3276.20797708183,939.876837895965,-3013.815820557,3347.26594466882,-1641.06044939735,-1016.84920399738}
WL:={1660,1680,1715,1735,1805,1810,1840}
mSpec:={{1,0.61013037,0.610615253,0.613445401,0.613648176,0.610915303,0.610187292,0.605716109},
{1,0.588049471,0.588013291,0.5908373,0.591266096,0.588798761,0.588066161,0.583659887},
...
Table[mSpec[[i ;; i, 1 ;; 8]].Parms, {i, 1, 154}]
The Copy Prediction Evaluations for Excel reproduces the Excel export of the Save Summary and X-Predictor Data As... option in the File menu, except that the exported information, including the model formula, is copied directly to the clipboard. This can be copied into the first cell of any sheet in an open Excel file; the block must be started in the first cell of a given sheet for the formula to be valid.
The Copy Prediction Evaluations for C++ will place C++ text on the clipboard. When pasted into the VC++ compiler environment and incorporated into a C++ app, this will create an executable containing the computations of the predictions. This does include C++ evaluation code for the current model.
#include "stdafx.h"
double Parms[9]={3.80101628699495,-1127.38241924426,2239.66389164645,1661.60706884307,-2967.54898268597,-2186.35921274612,2409.10820305251,2564.84006162749,-2597.65191762715};
double WL[8]={1650,1680,1715,1735,1760,1775,1805,1820};
double mSpec[154][8]={
{0.611359596,0.610615253,0.613445401,0.613648176,0.614745677,0.614739835,0.610915303,0.608658373},
...
double glmEval(int nx, double *parms, double *spec)
{
double estimate = parms[0];
for(int i=1; i<=nx; i++)
estimate += parms[i]*spec[i-1];
return estimate;
}
double *glmEvalAll()
{
int nobs = 154;
int nx = 8;
double *estimate = (double *)calloc(nobs, sizeof(double));
for(int i=0; i<nobs; i++)
estimate[i] = glmEval(nx, Parms, mSpec[i]);
return estimate;
}
Note : For all of the language code options, the X-predictor identifications (WL, Wn, or index) are saved in a WL array even though it is not used in the prediction evaluations. While the Parms array is obviously model-specific, the same is true of the mSpec spectral matrix since only the X-predictors used in the model are written.
Style Menu
The Font Select item is used to set the Font that is used in the summary.
The Color item enables or disables the color formatting in the summary.
The HTML Format option may be of value in pasting portions of the summary into an HTML editor. This option replaces spaces in the text with no-break spaces.
Outliers Menu
The Flag Standardized Residuals Outliers mark data as probable outliers. The File menu's Save Data w/Inactive Observations Removed will omit these data in writing a new data matrix file.
Use the Multiples of SE options of Outside of 2 SE, Outside of 3 SE, and Outside of 4 SE to set the bounds for detection.
Sort Menu
Since the prediction data have no connection to the fitting, you can optionally sort the prediction data by Increasing Y Data, Increasing Y Predicted, and Increasing Residuals.
 |