PeakLab v1 Documentation Contents AIST Software Home AIST Software Support
Numeric Summary
This option is accessed from the Review's Numeric option. It is used to display all numerical peak analysis information. The Numeric Summary window is live and can remain up while different data sets are selected or deselected in the Review.
The View Numeric Summary for this Fit right click popup menu option opens the Numeric Summary with only the content for the specific fit where this right click popup was invoked. If the window is already open, it is updated with just this specific fit.
This numeric summary can consist of the following items, all selected from the Options menu:
· Fitted Parameters - goodness of fit and fitted parameter values
· Equivalent Parameters - for GenHVL and GenNLC models, the equivalent diffusion-kinetic parameters
· Measured Values - measured peak characteristics; also includes analytic areas if available
· Analytic Moments - the analytic moments of the model
· Deconvolved Moments - the moments of the deconvolutions inherent in a model
· Advanced Area Analysis - additional information in breakdown of components of areas
· Parameter Statistics - peak by peak parameter statistics
· Chromatography Analysis - theoretical plates and resolutions
· Overlap Areas - matrix of overlap areas for all peaks
· Analysis of Variance - ANOVA
· Details of Fit - Convergence State, Iterations, Fit Settings
· Average Multiple Fits - Averages of Coefficients of Variations of multiple similar fits
The Options menu also includes:
· Add Probabilities - adds probability values to the parameter statistics and analysis of variance table
· Add X Area Values - adds the x values at specific cumulative areas for supported models
· 90 %Confidence - uses 90% confidence levels for parameter statistics
· 95 %Confidence - uses 95% confidence levels for parameter statistics
· 99 %Confidence - uses 99% confidence levels for parameter statistics
· Specify Column Dead Time - offers input of dead-time for the specific retentions reported in chromatographic summary if x values were not transformed
The Options menu also includes menu options for selecting a predefined set of options:
· Select All - all sections will be included
· Select Only Fitted Parameters - only the Fitted Parameters section will be included
· Select Chromatography - Fitted Parameters, Equivalent Parameters, Measured Values, Analytical Moments, Deconvolved Moments, Advanced Area Analysis, Chromatography Analysis, Overlap Areas
· Select Statistical - Fitted Parameters, Measured Values, Analytical Moments, Parameter Statistics, ANOVA - Analysis of Variance, Add Probabilities
All elements of this Numeric Summary are computed when the Review is opened with the exception of Overlap Areas. Because this is a matrix of integrations, it can require a considerable time with a large number of peaks or with those that are particularly demanding to compute. Overlap Areas should not be routinely checked unless you really need this information.
The Numeric Summary is toggled on and off by the Numeric button in the Review. The window size and position you choose for the Numeric Summary is automatically saved across sessions. The Numeric Summary uses the PeakLab RTF Viewer to display, modify, and print the information.
Viewing/Averaging only Selected Fits
When multiple data sets are fitted, you can view (and average) only specific fits in the Numeric Summary. The selection process must be done in the Review window. It cannot be done directly within the Numeric Summary window.
Procedure in Review to Select Fits
These instructions apply to the Review window. If you wish to compare/average only certain fits in the Numeric Summary, select those you wish to review by clicking on the specific graph for that fit (the border will turn gray to indicate selection). You can also use the Select this Graph right click menu option for each fit. You can click again on a selected set to deselect it, or use Unselect this Graph from the right click popup menu. When the sets you wish to individually review are selected, select the Plot | Only Selected Fits from the right click menu. Only those data fits will be rendered in the Review graphs, in the Numeric Summary, in the Residuals, in the Explore option, and in the Export.
If you only wish to review one of the fits, you can double click that graph to open a review of just that fit. You can also choose Plot this Fit (or Plot Only this Fit) from the right click menu. When you are finished, and you wish to restore all of the fits, you can once more double click the graph or select Plot All Fits.
Averaging Different Fits without Refitting
If the data sets are identical in peak count, peak model, and in how they were fitted, the Average Multiple Fits will produce useful values for a standard. If you wished run a concentration series for a standard, for example, you can fit all of these data sets in one step and use this selection in the Review to have only those selected sets displayed in the Numeric Summary. The averages and CVs will be automatically updated to reflect those selections. There is no need to create different data files or execute separate fits. Simply select the fits you wish to view and these will be displayed and averaged in the Numeric Summary.
Fitted Parameters
The Fitted Parameters section begins with PeakLab's sum of squares based goodness of fit criteria. These are the rČ coefficient of determination, a degree of freedom adjusted rČ, the standard error for the fit, the F-statistic for the fit, and the ppm unaccounted variance. The summary then presents each function and its fitted parameter values. If a background was fitted, it is last in the function list.
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
0.99991477 0.99991466 0.00968436 9,571,866 85.2295102
Peak Type a0 a1 a2 a3 a4
1 GenNLC 2.01452745 3.05122094 0.00024861 -0.0031843 1.14665629
2 GenNLC 0.57304194 4.90636059 0.00030115 -0.0006486 1.14665629
3 GenNLC 0.66842649 5.89144460 0.00030732 -0.0004125 1.14665629
4 GenNLC 0.30453186 9.32507941 0.00047594 0.00031223 1.14665629
5 GenNLC 1.06248152 21.7583350 0.00119313 0.01094087 1.14665629
6 GenNLC 0.60317688 27.4861040 0.00143410 0.00832760 1.14665629
The goodness of fit statistics are as follows:
N = count of data observations
np = count of parameters
DOF = degree of freedom, N-np
SSE = sum of squared errors from the fit
SSM = sum of squares about the mean of the dependent variable
MSR = mean square regression
MSE = mean square error
rČ Coef Det (rČ Coefficient of Determination)
DF Adj rČ (Degrees of Freedom Adjusted rČ Coefficient of Determination)
![]()
Fit Std Err (Fit Standard Error)
F-value (F-statistic)
![]()
ppm uVar (unaccounted variance, parts per million)
![]()
If a peak parameter fails significance, the parameter for that peak will be grayed. This furnishes immediate feedback that a model may be overspecified (that a more complex model has been fitted than the data can support). Bear in mind that significance is a test for a non-zero value. For certain parameters in certain peak models, a failed significance reflects an ideal peak. For example, the a4 asymmetry in the GenHVL model will not be different from zero if the peak is seen by the fitting as close to perfectly symmetric in the third moment of the core density.
Equivalent Parameters
For a GenHVL model, this section converts the parameters from a diffusion-based HVL model to a kinetics-based NLC, furnishing the equivalent parameters had you chosen to make a GenNLC fit. For a GenNLC model, this section converts the parameters from a kinetics-based NLC model to a diffusion-based HVL, furnishing the equivalent parameters had you chosen to make a GenHVL fit.
Equivalent Parameters
Peak Type a0 a1 a2 a3 a4
1 GenHVL 2.01452745 3.05122094 0.03894996 -0.0031843 0.01463749
2 GenHVL 0.57304194 4.90636059 0.05436082 -0.0006486 0.01270456
3 GenHVL 0.66842649 5.89144460 0.06017585 -0.0004125 0.01171207
4 GenHVL 0.30453186 9.32507941 0.09421421 0.00031223 0.01158503
5 GenHVL 1.06248152 21.7583350 0.22786153 0.01094087 0.01200822
6 GenHVL 0.60317688 27.4861040 0.28077663 0.00832760 0.01171335
Measured Values
The initial Measured Values section uses minimization and root-finding algorithms to report amplitude, center (mode or apex), full width at half-maxima (FWHM), asymmetry at half-maxima (Asym50), full width at 10% of maxima (FW Base), and asymmetry at 10% of maxima (Asym10) measured values.
The final Measured Values section first reports an integrated area and its percentages. The integrated area is computed from the minimum X of the fitted data to the maximum X of the fitted data. Note that the integrated area will be less than the analytic area if some portion of that peak is outside this X range of the data. The final four elements are the first, second, third, and fourth moments. The second moment is reported as an SD instead of a variance. The area and moment computations use an automated integration routine which uses a Gaussian Quadrature or Romberg method. Target precision is 1E-8.
Measured Values
Peak Type Amplitude Center FWHM Asym50 FW Base Asym10
1 GenNLC 17.8716084 3.14096487 0.10664365 0.48899022 0.21451372 0.42773806
2 GenNLC 4.16502418 4.92863684 0.12935111 0.88416960 0.25864659 0.86456084
3 GenNLC 4.41042518 5.90649497 0.14244138 0.93009104 0.28489828 0.92035906
4 GenNLC 1.29103598 9.31113024 0.22152812 1.05741417 0.44380373 1.08094057
5 GenNLC 1.77954450 21.3677392 0.55844785 1.75524682 1.14463028 2.02141201
6 GenNLC 0.84359492 27.1673938 0.66972658 1.45557636 1.35828714 1.61026579
Peak Type Area % Area Mean StdDev Skewness Kurtosis
1 GenNLC 2.01452745 38.5467988 3.11407765 0.04686849 -0.5508965 2.97230910
2 GenNLC 0.57304194 10.9648208 4.92282943 0.05490883 -0.1112859 2.99210316
3 GenNLC 0.66842649 12.7899480 5.90283072 0.06044843 -0.0589339 2.99493096
4 GenNLC 0.30453186 5.82703808 9.31637063 0.09421028 0.08095826 3.00760983
5 GenNLC 1.06248152 20.3299594 21.4872108 0.24940648 0.53909101 3.10909761
6 GenNLC 0.60317687 11.5414348 27.2649660 0.29211223 0.40048612 3.07535479
All Total 5.22618613 100.000000
Analytic Moments
An analytic moment is one which has a closed form solution. PeakLab has closed form analytic moment formulas for many of its peaks functions. Unfortunately, we do not have formulas for the GenHVL and GenNLC families of models. When an analytical moment is not available, the analytic moments will be given for the ZDD (zero-distortion density) of the GenHVL or GenNLC model:
Analytic Moments
Peak Type FnArea % FnArea FnMean FnStdDev FnSkewness FnKurtosis
1 GenNorm[m] 2.01452745 38.5467987 3.05122094 0.03895622 0.04391796 3.00342915
2 GenNorm[m] 0.57304194 10.9648208 4.90636059 0.05436740 0.03811728 3.00258309
3 GenNorm[m] 0.66842649 12.7899480 5.89144460 0.06018204 0.03513903 3.00219519
4 GenNorm[m] 0.30453186 5.82703806 9.32507941 0.09422369 0.03475781 3.00214782
5 GenNorm[m] 1.06248152 20.3299594 21.7583350 0.22788617 0.03602769 3.00230764
6 GenNorm[m] 0.60317688 11.5414351 27.4861040 0.28080552 0.03514286 3.00219567
All Total 5.22618614 100.000000
In this case, the moments for the generalized normal with a1=mean, the ZDD, are given. When the Measured Values and Analytic Moments section use the same model, unless some portion of a peak extends beyond the X-range of the data, the analytic and numeric integration areas will be essentially equivalent.
The baseline is not included in this option.
Deconvolved Moments
A given model will have its own specific deconvolutions or simplifications. If an <irf> instrument response function model is fitted, the first deconvolution will be the peak absent this IRF. There will then be a succession of up to two additional deconvolutions. In this example where the IRF was presubtracted and a GenNLC fitted, the moments are for the pure NLC, the peak absent the ZDD adjustments for nonideality, and the Giddings, the peak absent all chromatographic distortion, the expected peak at infinite dilution.
Deconvolved Moments
Peak Type Area Mean StdDev Skewness Kurtosis
1 NLC 2.01452745 3.11359553 0.04638333 -0.5754550 3.01434309
2 NLC 0.57304194 4.92280794 0.05481415 -0.1327280 2.99963882
3 NLC 0.66842649 5.90282199 0.06038679 -0.0787251 2.99874389
4 NLC 0.30453186 9.31636798 0.09424530 0.06134788 3.00315182
5 NLC 1.06248152 21.4859511 0.25094228 0.51874259 3.07620833
6 NLC 0.60317687 27.2643081 0.29324707 0.38067153 3.05177301
Peak Type Area Mean StdDev Skewness Kurtosis
1 Giddings 2.01452745 3.05122094 0.03894996 0.01914805 3.00048886
2 Giddings 0.57304194 4.90636059 0.05436082 0.01661949 3.00036828
3 Giddings 0.66842649 5.89144460 0.06017585 0.01532116 3.00031298
4 Giddings 0.30453186 9.32507941 0.09421421 0.01515497 3.00030623
5 Giddings 1.06248152 21.7583350 0.22786153 0.01570857 3.00032901
6 Giddings 0.60317685 27.4861040 0.28077641 0.01531470 3.00027213
These are also numeric integrations similar to those used in the Measured Values section. Again, the integrated area will be less than the analytic area if some portion of that peak is outside this X range of the data, and the second moment is reported as an SD instead of a variance.
Advanced Area Analysis
In most cases, this Advanced Area Analysis section will furnish a measure of the deviation from the non-ideality furnished by the ZDD's higher moment parameters. This is especially useful for higher overload peaks or in instances where you would like to quantify these deviations.
Advanced Area Analysis
Peak Type Area % Area ApexAsym NonOverlap1 % PkArea NonOverlap2 % PkArea
1 GenHVL[Yp2]<e2> 323.654533 100.000000 0.47529501 225.535354 69.6839781 53.8177535 16.6281476
The Apex Asym furnishes the area asymmetry relative to apex or mode of the peak, the area to the right of the apex divided by the area to the left.
NonOverlap1 is the area of non-overlap between the peak with the ZDD non-ideality and the pure ZDD (the HVL or NLC deconvolved peak). In an overload peak, this is the difference between the peak with the overload shape (minus the IRF) and the deconvolved HVL, the peak that would theoretically exist if there were no overload or any other deviation from this ideality. For analytic peaks, this will be the difference between the GenHVL and HVL, or GenNLC and NLC, and in general, the removal of the ZDD non-idealities will result in only a small amount of non-overlap. In the example below, the non-overlap area is close to 70%. Only 30% of the deconvolved HVL's area is contained in the overload shape.
NonOverlap2 is the area of non-overlap between the peak with and without the IRF removed. In the example below, the area without overlap is 16.6%. One sixth of the overall area of the peak is without overlap between the two peaks.
If the fit is for an experimental two-state model, such as the GenHVL[Z|E], where there are two-components to the ZDD each of which contributes a portion to the overall area of a peak, the state 1 values will consist of the area for the D1 primary component in the (D1|D2) density, where state 2 will the the area for the secondary D2 density, the one adding the anomaly to the overall shape.
For certain models, you will also see a table similar to the following:
Peak Type x0.005 x0.01 x0.025 x0.05 x0.25 x0.50
1 GenHVL_C 4.46650032 4.54866980 4.67067048 4.77669246 5.09764104 5.29247708
Peak Type x0.50 x0.75 x0.95 x0.975 x0.99 x0.995
1 GenHVL_C 5.29247708 5.44831575 5.62480580 5.67771494 5.73919823 5.78142930
Peak Type xwa50 xwa90 xwa95 xwa98 xwa99
1 GenHVL_C 0.35067472 0.84811334 1.00704446 1.19052843 1.31492898
Peak Type x0.005 x0.01 x0.025 x0.05 x0.25 x0.50
1 HVL_C 4.48743900 4.56215809 4.67519812 4.77555231 5.09223273 5.29474252
Peak Type x0.50 x0.75 x0.95 x0.975 x0.99 x0.995
1 HVL_C 5.29474252 5.46283811 5.66029357 5.72103970 5.79256978 5.84230132
Peak Type xwa50 xwa90 xwa95 xwa98 xwa99
1 HVL_C 0.37060538 0.88474126 1.04584158 1.23041170 1.3548623
If the model is a GenHVL, or Gen2HVL, the Advanced Area Analysis will evaluate the roots of the GenHVL and HVL cumulatives to get the x values at .5%, 1%, 2.5%, 5%, 25%, 50%, 75%, 95%, 97.5%, 99%, and 99.5% area. If the model is the HVL, only the HVL cumulative is evaluated. The xwa50 through xwa99 values are the peak widths for areas of 50%, 90%, 95%, 98%, and 99%. Note that the xwa50 width will likely be very different from the FWHM (full width at half-maximum, 50% of the peak's amplitude) and the xwa90 width will likely be very different from the FW Base (width at 10% of the peak's amplitude).
If the model is a GenNLC or Gen2NLC, the GenNLC and NLC cumulatives will be evaluated. For the NLC, only the NLC cumulative is evaluated.
The x0.005-x0.995 values will only be shown if the Add X Area Values is checked in the Options menu.
Note that this Advanced Area Analysis only exists for these specific closed form cumulatives. If an <irf> version of one of these models is fitted, you will see these cumulatives absent the IRF, and those will represent the IRF Deconv. and Partial Deconv. deconvolution levels in the Review.
A center of mass is not reported for the model with the <irf> (a peak model that is itself not of a closed-form solution will not a have a closed-form cumulative). You can still manually get this center of mass of the eluted peak with the IRF present by using the Evaluate Fit Model right click menu option in the Review to integrate from a baseline x position prior to the peak to various x positions within the peak, seeking a value where exactly half the reported area is found.
If the peak area is proportional to mass, the mean or first moment of an asymmetric peak will not be the center of mass. You will need to use the x0.50 values from this Advanced Area Analysis for center of mass retention values.
For the GenHVL, Gen2HVL, GenNLC, and Gen2NLC models, a1 is the mean of the ZDD zero distortion density (either a generalized normal or generalized error model). This reflects a concentration independent location of the retention absent the a3 chromatographic distortion (the retention at infinite dilution), but it includes the deviation from theoretical ideality which is present in the ZDD. In the Measured Values section, the Center is the mode or apex of the peak as fitted, and the Mean is the first moment of the actual fitted peak. In the Deconvolved Moments section, the mean or first moment is given for the different deconvolutions.
Parameter Statistics
The Parameter Statistics section is a peak by peak display of parameter statistics, which include each parameter's value, standard error, t-value (parameter value/std error), and confidence limits. The confidence level is set in the Options menu. Note that these standard errors and confidence limits assume normal (Gaussian) errors. If you plan to use these statistics, you should confirm normal errors using a Residuals Graph, inspecting both a distribution and SNP plot.
Parameter Statistics
Peak 1 GenNLC
Parameter Value Std Error t-value 95% Conf Lo 95% Conf Hi P>|t|
Area 2.01452745 0.00018515 10880.4555 2.01416454 2.01489036 0.00000
Center 3.05122094 2.9614e-5 1.0303e+5 3.05116290 3.05127899 0.00000
Width 0.00024861 2.764e-7 899.444774 0.00024806 0.00024915 0.00000
Distortn -0.0031843 1.764e-6 -1805.1787 -0.0031877 -0.0031808 0.00000
NLCasym 1.14665629 0.01514743 75.6997452 1.11696604 1.17634653 0.00000
If a peak parameter fails significance, the parameter row for that peak will be grayed. You will be able to see the t-values used to test the significance. For a reasonably-sized chromatographic data set, 90% significance occurs around |t|=1.65, 95% significance occurs around |t|=1.96, and 99% significance occurs around |t|=2.58.
Chromatography Analysis
The Chromatography Analysis section includes the theoretical plates, retention, and resolution. These are described in the Chromatography Notes.
Theoretical Plates
There are four different computations of the theoretical
plate count offered by PeakLab. The Ngauss uses the traditional Gaussian approximation:
![]()
where Ctr is the time location at the center or apex and FWHM is the full width at half-maximum. This
conventional plate count definition assumes a Gaussian peak shape. Although a true Gaussian is seldom
seen in chromatography, by using only a center and FWHM, this plate count is robust insofar as it will
be less impacted by a high asymmetry or by a fattening of the tails. Moment-based methods use all of the
peak information, and can thus be strongly impacted by asymmetry and the fatness of the tails.
The Nmoment, Ndeconv, and Nmodel are based on the first and second central moments.
Unless analytic moments exist for the model, the mean and variance are calculated by numerical integration
of the noise-free parametric model:
![]()
The Nmoment theoretical plate estimate uses the first and second moments from the full fitted model. Everything in the observed peak is accounted, including the IRF distortions.
The Ndeconv estimate is the theoretical plate count for the first deconvolution, as it appears in the separate Deconvolved Moments numeric section. If an IRF-bearing model was fitted, this is the peak with the IRF mathematically removed (peak area is conserved). If a non-IRF closed-form model was fit, and if that model is a once-generalized or twice-generalized HVL or NLC, this first deconvolution in the Deconvolved Moments will be the pure HVL or NLC peak. For IRF-bearing models, the Ndeconv plate count estimates will typically be higher than the Nmoment values since the IRF distortions inflate the second moment. Note that fitting an implicit IRF in a closed-form model, such as the EMG or GMG, results in an Ndeconv for the deconvolved Gaussian.
The Nmodel theoretical plate estimate is based only on the a1 location and a2 width parameters from the model. In the case of a chromatographic model, a1 can be used for M1, the first moment, and a22 can be used for M2, the second moment. For a generalized HVL or NLC chromatographic model, this means the a3 concentration-dependent tailing-fronting and all third and higher moment core density nonidealities (asymmetry and compression/dilation) are removed in addition to the instrumental distortions. Since the Nmodel uses parametric estimates where all nonidealities are separately modeled for both the instrument and the column, this theoretical plate count represents the ideal, the maximum realizable from a separation with no instrumental distortions, and where the chromatographic broadening will be perfectly symmetric. Improvements in formulation and separation which reduce the peak asymmetry, or concentration reductions which lower the chromatographic fronting-tailing, should minimally impact the Nmodel estimate.
For the NLC-based models, the equivalent parameters computations are used to convert the NLC's kinetic width to a statistical standard deviation. The GenHVL and GenNLC models will thus produce equivalent Nmodel values for an identical goodness of fit. For models that are not HVL or NLC based, the full second moment is used, and the IRF, zero-distortion density asymmetry, and concentration-dependent tailing-fronting will be reflected in the Nmodel theoretical plate estimate. If the IRF fits to a significant tailing, the N in this instance may be substantially smaller since those tails can appreciably increase the second moment.
Retention
The retention column contains the thermodynamic retention factor. This will be the a1 value of the fitted peaks. If the x-values were not transformed for dead-time in a transform applied prior to fitting, you can still report the k capacity factor by using the Specify Column Dead Time in the Options menu. The Retention value is adjusted for this dead time. If you have pre-transformed the data for a Retention scale, do not enter a dead time in the Numeric Summary Options menu since the a1 parameter values will already reflect the retention factor values. Also note that this specification of a column dead time in this Numeric Summary only impacts the values reported in the Retention column. An untransformed time-scale fit is in no way altered.
Resolution
The next columns contains the resolution between adjacent peaks. There are two different resolutions reported, the standard FWHM method Res(HW) and a moment-based estimate Res(Stat). The moment-based estimates use the full fitted model of the observed peak.
![]()
![]()
fracNL
The last column contains the fraction to which each peak is in the nonlinear chromatography regime based upon the HVL mathematics. The fraction to which a peak is within the nonlinear chromatographic tailing/fronting is derived directly from the HVL model:
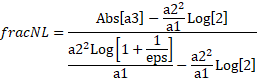
This is based on solving the following term in the denominator of the HVL for 0 and 1-epsilon:
![]()
For chromatographic data, which is typically collected to about 4 digits of precision, eps is set to 0.0001. This fracNL value is only reported for HVL, GenHVL, and Gen2HVL models. When this value is below 0, it means the nonlinear regime hasn't yet started and there us still room to increase the concentration for this component and still remain within the linear chromatographic regime. If the value is greater than 1, it means this term in the HVL denominator has essentially reached an asymptote and the model's conservation of mass will change the peak toward a sharp right triangular shape with a significant inflation of the FWHM.
Using the Different Theoretical Plate Values
The two chromatographic analyses that follow are from identical IC separations where the only difference is the concentration of six different analytes.
Chromatographic Analysis
Peak Type Nmoment Ndeconv Nmodel Ngauss Retention Res(HW) Res(Stat)
1 GenNLC<ge> 2504.99051 5002.11487 5010.51984 3921.04482 4.47743284
2 GenNLC<ge> 4739.09980 7510.73037 7513.74262 6163.23332 7.48559166 8.27738043 6.92939876
3 GenNLC<ge> 6095.41191 9097.81056 9103.18638 7566.33546 9.08821645 3.76758884 3.33530733
4 GenNLC<ge> 7896.33341 9491.13108 9486.90423 8503.76005 14.7358867 10.2413060 9.56236195
5 GenNLC<ge> 6749.52129 7121.75880 7179.73197 6792.08965 24.3461603 10.2413663 10.0850580
6 GenNLC<ge> 7623.88160 7989.53485 8075.43786 7648.24633 27.7222450 2.69043687 2.68660934
Chromatographic Analysis
Peak Type Nmoment Ndeconv Nmodel Ngauss Retention Res(HW) Res(Stat)
1 GenNLC<ge> 729.030401 805.845862 3868.76802 957.420876 4.30449113
2 GenNLC<ge> 3461.82826 4392.89691 5879.70170 4552.73768 7.40283975 4.54272586 4.25769488
3 GenNLC<ge> 5210.43069 6726.00944 7717.76995 6550.26389 9.02836123 3.23714757 2.90358801
4 GenNLC<ge> 6219.66960 6992.48115 9172.77375 6713.04722 14.6654122 8.59422124 8.19128381
5 GenNLC<ge> 2816.17907 2864.99435 7152.23940 3380.17804 24.3104437 7.38877835 6.99143585
6 GenNLC<ge> 1613.59862 1623.49824 6833.08700 2028.13802 28.1266972 1.43592020 1.39785980
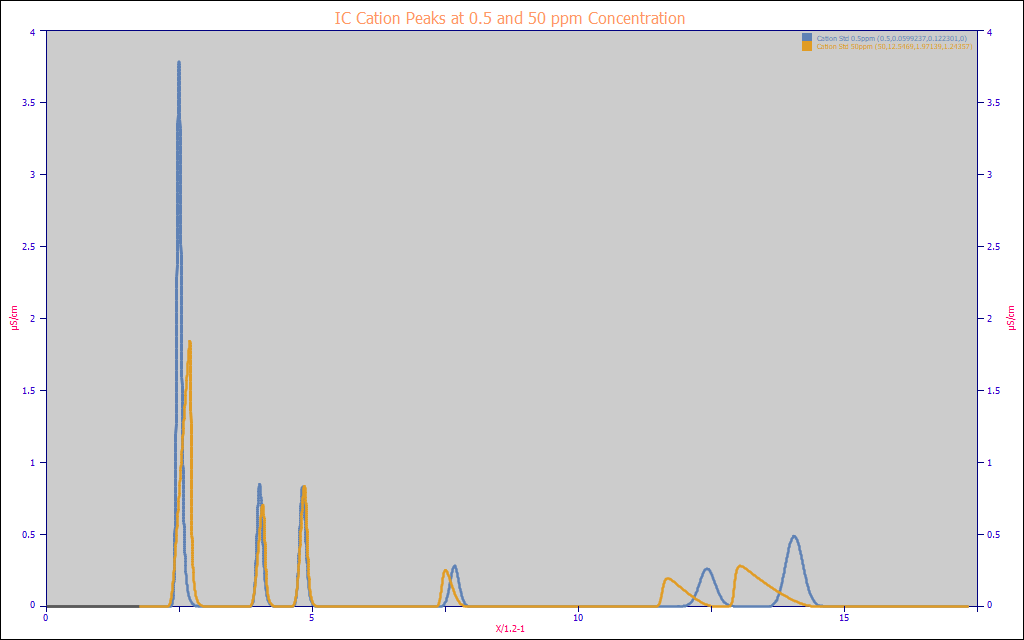
The first table uses 1/10x the normal analyte concentrations and the second table uses 10x the normal concentrations. Area normalized chromatograms for these analyses are in the above plot. The first table reflects very close to Gaussian peaks plus the instrumental distortions, the blue data. The second table reflects peaks with very high a3 tailing and fronting, the amber data. In these data, Peak 1 is a very early eluting narrow width fronted peak and Peak 6 is a very late eluting much wider tailed peak. Peaks 3 and 4 elute at intermediate times with far less fronting or tailing. The IRFs or instrument distortions are close to identical for each of the peaks at both concentrations.
The Ngauss plate count, using only the FWHM for the broadening, is somewhat more robust than the full moment estimates since much of the IRF and tailing-fronting impact the peak well below the half-maximum. Use the Ngauss estimate for conventional comparisons.
The Nmoment, at the low concentrations, reflects the higher impact of the IRF on the narrower first and second peaks. At the high concentrations, the strongly fronted and tailed peaks show a serious loss in estimated efficiency that correlates with the magnitude of tailing or fronting. The second moment is strongly impacted by the IRF and by significant a3 tailing or fronting. Use the Nmoment estimate of theoretical plates for an efficiency that includes instrumental distortions, tailing-fronting from concentration effects, and peak asymmetry arising from nonideality in the media and packing.
The Ndeconv plate count estimates above exclude the fitted IRF. While not quite constant across the six peaks, at the low concentration the Ndeconv estimates are much stabler. At the high concentration, however, the tailing and fronting still produce the same sharp differences with the more linear chromatographic shapes at the low concentration. When you have fitted an IRF, use the Ndeconv estimate of theoretical plates for a measure of the efficiency with the IRF removed.
The Nmodel plate count uses the estimated a2 broadening from the fitted model, removing the chromatographic tailing and fronting reflected in the a3 distortion of a chromatographic model. As you will note, there is now a much better stability across the six peaks irrespective of concentration. Use the Nmodel estimate of theoretical plates as a measure of efficiency with the IRF and the a3 tailing and fronting concentration effects removed. If a generalized model, such as the GenHVL, is fitted, any impact on the efficiency from a higher moment deviation from the Gaussian of the pure HVL or the Giddings of the pure NLC is also removed.
Overlap Areas
The Overlap Areas section consists of a square matrix whose size is the peak count. This option can be quite time consuming with a large number of peaks or with peaks whose functions are computationally demanding. To find the overlap area between any two peaks simply find the desired position in the matrix. The computations use an automated integration routine which uses a Gaussian Quadrature or Romberg method. Target precision is 1E-8.
Overlap Areas
Peak Type Peak 1 Peak 2 Peak 3 Peak 4 Peak 5 Peak 6
1 GenNLC 2.01452745 5.1385e-87 4.973e-178 0.00000000 0.00000000 0.00000000
2 GenNLC 5.1385e-87 0.57304194 6.3064e-18 4.86e-202 0.00000000 0.00000000
3 GenNLC 4.973e-178 6.3064e-18 0.66842649 1.606e-113 0.00000000 0.00000000
4 GenNLC 0.00000000 4.86e-202 1.606e-113 0.30453186 0.00000000 0.00000000
5 GenNLC 0.00000000 0.00000000 0.00000000 0.00000000 1.06248152 1.1842e-29
6 GenNLC 0.00000000 0.00000000 0.00000000 0.00000000 1.1842e-29 0.60317687
In the diagonals of the matrix are the actual areas of the peaks.
Analysis of Variance
The Analysis of Variance section includes a standard ANOVA table and also reports the rČ coefficient of determination, the degree of freedom adjusted rČ, and the standard error for the fit (the square root of the Mean Square Error).
Analysis of Variance
r2 Coef Det DF Adj r2 Fit Std Err
0.99991477 0.99991466 0.00968436
Source Sum of Squares DF Mean Square F Statistic P>F
Regr 21545.171207352 24 897.71546697301 9571866.1517028 0.0000000000
Error 1.8364409071549 19581 9.37868805e-5
Total 21547.007648259 19605
Details of Fit
The Details of Fit section is helpful for subsequently referencing how a fit was made, and its success or failure relative to convergence. Also reported are the number of parameter constraints violated on the final iteration. Many of the items summarize the current Fit Preferences since these can significantly affect the results of any given fit.
Details of Fit
Set Convergence State Iterations Minimization Curvature Matrix GA Prefit GA Conv
1E-6 Converged 10 Least Squares Sparse-Roots None 6
Constraint a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 Fail
Local 25.00 5.00 50.00 None None None None None None None 0
Global None None None None None None None None None None
Average Multiple Fits
The Average Multiple Fits section is only available where there are multiple fits and those can averaged. All must have exactly the same peak count and use the same model, and there must be no customizations, as in locking a parameter in one fit but not another.
When this option is selected, and averaging is permitted, you will see two separate numeric summaries at the end of summaries for the individual data sets. The first will contain the averages, there will be no data set information, and a title similar to "Average for 12 Fits" will precede a summary where every value is an average of the values from all of the individual summaries. You will need to use caution with respect any value arising from a parameter in one data set that happens to fit to a wild value that severely distorts the average.
The second numeric summary at the end of the individual data set summaries will contain the CV% (coefficient of variation percentages), there will again be no data set information, and a title similar to "CV Percent for 12 Fits" will precede a summary where every value in that summary is a CV% from the averages of the individual summaries. A CV is simply the SD/mean, here expressed as a percent. You will need to be cautious here since these will be CV percentages whose values will look strange inserted into the same exact Numeric Summary format. When averaging multiple analyses, this format allows you to see all of the variability in one view. It may take some getting used to, but we have found it helpful to see with effortless immediacy which parameters within an average are most tightly determined and which are more variable, and in a % format where everything is comparable.
This averaging can be useful for creating standards. In the example that follows, we took a standard run at three different times with varying columns and column age, and at various concentrations, and fit these in a single step. Using the fit selection described at the beginning of this topic, we automatically averaged the three sets at three different concentrations to see if the variability was lessened at higher sample concentration.
5ppm
Average for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
0.99999176 0.99999174 0.00361099 50,008,399 8.23618667
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 1.77357298 2.33640185 0.00024239 -0.0022886 1.17011522 0.00659790 0.04324097 0.61185853
2 GenNLC<ge> 0.49582206 3.79381822 0.00027024 -0.0003633 1.17011522 0.00659790 0.04324097 0.61185853
3 GenNLC<ge> 0.57367978 4.56474247 0.00026385 -0.0001801 1.17011522 0.00659790 0.04324097 0.61185853
4 GenNLC<ge> 0.25930420 7.26517653 0.00038954 0.00029395 1.17011522 0.00659790 0.04324097 0.61185853
5 GenNLC<ge> 0.43847415 11.9222856 0.00081624 0.00281495 1.17011522 0.00659790 0.04324097 0.61185853
6 GenNLC<ge> 0.89753559 13.5566498 0.00087205 0.00617092 1.17011522 0.00659790 0.04324097 0.61185853
CV Percent for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
4.5945e-5 4.6074e-5 3.31584855 5.75911264 5.57691676
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 0.93704162 0.44733312 1.61674263 0.80244269 14.7176342 14.9444496 1.35253140 1.76572075
2 GenNLC<ge> 1.10525181 0.10674379 0.75401308 4.10251401 14.7176342 14.9444496 1.35253140 1.76572075
3 GenNLC<ge> 1.59853985 0.14221774 0.10465515 6.83408844 14.7176342 14.9444496 1.35253140 1.76572075
4 GenNLC<ge> 1.18375811 0.49254277 0.39443729 7.51451576 14.7176342 14.9444496 1.35253140 1.76572075
5 GenNLC<ge> 1.00553087 0.61434321 0.73820553 2.05882070 14.7176342 14.9444496 1.35253140 1.76572075
6 GenNLC<ge> 1.24164589 0.77370110 0.65903115 1.76584386 14.7176342 14.9444496 1.35253140 1.76572075
10ppm
Average for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
0.99999203 0.99999201 0.00675034 51,723,654 7.97274523
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 3.53790243 2.32065496 0.00022910 -0.0044989 1.25254712 0.00867667 0.04331777 0.62286980
2 GenNLC<ge> 0.98894059 3.78785288 0.00027418 -0.0006667 1.25254712 0.00867667 0.04331777 0.62286980
3 GenNLC<ge> 1.14553797 4.56064618 0.00026515 -0.0002762 1.25254712 0.00867667 0.04331777 0.62286980
4 GenNLC<ge> 0.51944067 7.26246876 0.00039374 0.00083459 1.25254712 0.00867667 0.04331777 0.62286980
5 GenNLC<ge> 0.87895741 11.9127144 0.00081961 0.00583762 1.25254712 0.00867667 0.04331777 0.62286980
6 GenNLC<ge> 1.80027348 13.5676007 0.00089807 0.01258912 1.25254712 0.00867667 0.04331777 0.62286980
CV Percent for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
5.7016e-5 5.7197e-5 3.14069349 7.03282761 7.15684149
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 1.19031673 0.40975167 0.65897871 0.40864655 3.91202616 5.40931380 0.48895763 1.56800196
2 GenNLC<ge> 1.37221451 0.08045825 0.77476572 2.92067435 3.91202616 5.40931380 0.48895763 1.56800196
3 GenNLC<ge> 1.55592047 0.14689382 0.28231932 8.19606519 3.91202616 5.40931380 0.48895763 1.56800196
4 GenNLC<ge> 1.35544799 0.52143216 0.32934378 2.95440225 3.91202616 5.40931380 0.48895763 1.56800196
5 GenNLC<ge> 1.13461344 0.54187712 0.44634291 1.39547291 3.91202616 5.40931380 0.48895763 1.56800196
6 GenNLC<ge> 1.18984591 0.70939707 0.37598270 1.49405036 3.91202616 5.40931380 0.48895763 1.56800196
25ppm
Average for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
0.99999225 0.99999223 0.01434474 61,756,358 7.74812769
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 8.83233211 2.29415896 0.00025133 -0.0109638 1.15099760 0.00881069 0.04291114 0.62827947
2 GenNLC<ge> 2.46684920 3.77587739 0.00028988 -0.0017208 1.15099760 0.00881069 0.04291114 0.62827947
3 GenNLC<ge> 2.86442829 4.55441389 0.00027141 -0.0007872 1.15099760 0.00881069 0.04291114 0.62827947
4 GenNLC<ge> 1.29272307 7.26904435 0.00039498 0.00231398 1.15099760 0.00881069 0.04291114 0.62827947
5 GenNLC<ge> 2.19303204 11.8787540 0.00081253 0.01410057 1.15099760 0.00881069 0.04291114 0.62827947
6 GenNLC<ge> 4.48819833 13.5868866 0.00092725 0.03086562 1.15099760 0.00881069 0.04291114 0.62827947
CV Percent for 3 Fits
Fitted Parameters
r2 Coef Det DF Adj r2 Fit Std Err F-value ppm uVar
0.00040330 0.00040432 26.2107987 40.9118570 52.0513290
Peak Type a0 a1 a2 a3 a4 a5 a6 a7
1 GenNLC<ge> 0.94020389 0.47187826 2.62482703 0.02801510 0.63021840 4.51584163 0.41439057 1.10829081
2 GenNLC<ge> 0.96980623 0.10394166 0.84639105 1.46689038 0.63021840 4.51584163 0.41439057 1.10829081
3 GenNLC<ge> 0.88288359 0.14607492 0.12781207 5.09615289 0.63021840 4.51584163 0.41439057 1.10829081
4 GenNLC<ge> 1.14343169 0.49102902 0.37273890 3.52361828 0.63021840 4.51584163 0.41439057 1.10829081
5 GenNLC<ge> 0.79244735 0.56182612 0.54549374 1.47090685 0.63021840 4.51584163 0.41439057 1.10829081
6 GenNLC<ge> 0.82300983 0.72613558 0.92480419 1.54897793 0.63021840 4.51584163 0.41439057 1.10829081
The advantage of our unusual layout should be more apparent in this example. The test was done at three different concentrations, 5ppm, 10ppm, and 25ppm.
The a0 areas have a slightly better CV% at the higher concentration. The a1 average center values and CV% are little impacted by concentration nor are the averaged a2 time constants. The CV% for a2 looks better at the 10ppm concentration. The a3 distortion is close to linear with concentration. The a3 CV% improve with concentration.
The a4 higher moment ZDD parameter CV% is significantly improved at higher concentration (the greater the strength of the intrinsic chromatographic asymmetry arising from a3, the better a4 is estimated). Here we see that the half-Gaussian component of the IRF, a5, is somewhat impacted by concentration, and it also improves in its CV% with higher sample concentration. The exponential component of the IRF, a6, also becomes less variable with concentration, but here we can see in one quick look that the 'g' component of the <ge> IRF is about 10x more variable than the 'e' component. We can also note that we are computing the shared exponential width in the IRF almost as accurately as the a1 center values of the peaks. The area fraction of the 'g' component of the IRF, a7, is also close to constant in its averages, but the CV improves somewhat with higher concentration. If we look at the goodness of fit averages, there is only the slightest improvement with concentration, and the variability worsens.
While there might be many ways to interpret the information, the improved CV percentages with concentration are clearly apparent. If the a4 higher order ZDD parameter, and the a5 and a6 IRF parameters, were tied to column/instrument health, the reduction in variability in these higher concentration estimates would be important.
Database/Excel Export
The File menu of the numeric summary contains a Save Extract for Database option. This will write the numeric summary to a CSV format suitable for database or Excel import.


 |