PeakLab v1 Documentation Contents            AIST Software Home            AIST Software Support

IRF Deconvolution

The IRF Deconvolution button or the Deconvolve Instrument Response Function menu item in the main window Data menu opens the procedure for the IRF deconvolution preprocessing of data.

You can also use the Deconvolve Instrument Response Function icon in the main program toolbar.

Deconvolution and Convolution

This procedure offers both deconvolution and convolution. In simplest terms, convolution is the smearing of a data set by a given instrument response function. Deconvolution is the procedure of undoing that smearing in an effort to see what the data would look like had the instrument perfectly rendered it.

IRF Deconvolution in Non-Gradient Peaks

For conventional chromatographic peaks, this procedure will mainly be used to subtract or remove the instrument response function from data prior to fitting. This processing of sharpening the data to remove instrumental/system smearing or distortions will use the Deconvolve options in this procedure.

The IRF Determination by fitting a convolution model is extensively discussed in the IRF Estimation 1 - Standards Containing One or More 'Fronted' Peaks, IRF Estimation 2 - Standards Sectioned to Contain Only Fronted Peaks, IRF Estimation 3 - Standards Containing Only Tailed Peaks topics. You can estimate the IRF parameters by fitting an <irf> convolution model or alternatively, by a genetic algorithm optimization of the deconvolution directly in this procedure. Once an IRF has been accurately estimated, the IRF deconvolution preprocesses the data, removing the instrumental/system distortions. This is often the last step in the sequence of preparing the data for fitting.

When this IRF deconvolution is done in this preprocessing step, you will only fit closed form models (no <irf>convolution model is used). The advantages of this deconvolution step include closed-form fits which are nearly immediate, and you can have an effective instrumental distortion removal for data sets which are too messy for fitting a model with an <irf>, such as those with overlapping and hidden peaks. An <irf> model fit involves a non-closed-form convolution (an integral) which fits much more slowly, even though all of the cores available in your machine are used in separate simultaneous threads (parallel processing).

Gradient Convolution in HPLC Gradient Peaks

For HPLC gradient peaks, this procedure will mainly be used to unwind the compressed gradient peak to produce the peak that one would see if no gradient were present. This process of undoing the impact of the gradient will use the Convolve options in this procedure. The process of using convolution to 'unwind' the gradient is covered extensively in the HPLC Gradient Peaks topic. The alternative of fitting the fourth moment kurtosis using the twice generalized Gen2HVL and Gen2NLC models is also covered in the HPLC Gradient Peaks topic.

Fourier Signal Processing Requirements

Because a Fourier signal must be continuous, zero at both bounds, to not introduce 'ringing', a baseline correction step should always precede the Fourier processing. This applies to both deconvolution and convolution. Feel free to be generous with the amount of baseline on each side of the peaks.

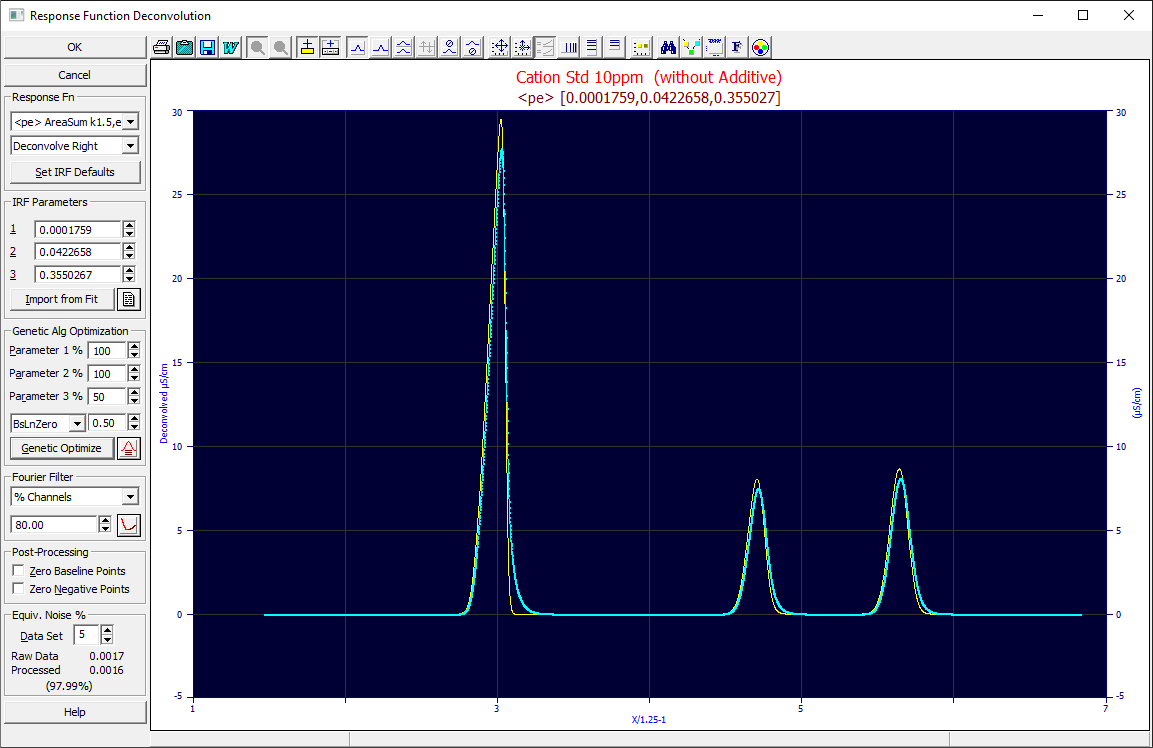
Response Function

The IRF model is selected in the first dropdown.

IRF Deconvolution in Non-Gradient Peaks

We recommend that you start with the <ge>, <pe>, or <e2> model for both LC and GC as the IRFs most likely to match real-world IRF distortions. When an IRF is selected, the current default parameters for that IRF are placed in the IRF Parameters fields. The IRF direction is set in the next dropdown. The Deconvolve Right will be the one used for chromatography IRFs. The program includes the spectral functions for fitting UV/VIS channel data, and if you are processing an IRF in spectroscopy data, you will need to use the Deconvolve Two-Sided option. For spectral data, use the <g> to deconvolve the Gaussian component, and use the <s> Student's t with the nu set to 1.0 to deconvolve the Lorentzian component.

Gradient Convolution in HPLC Gradient Peaks

We recommend that you start with the <g> or <k> model for unwinding the gradient. When the response function model is selected, the current default parameters for this specific IRF are placed in the IRF Parameters fields. For this function, you will select the Convolve Right option. Note that the default <g> and <k> IRF parameter values will be those we found of value with conventional LC peaks. For gradient peaks, we suggest a <g> half-Gaussian SD of 0.018 in retention units. For the <k>, we recommend a 0.7 fractional order and 0.02 for the time constant width, again in retention units (the t/t0-1 dead time adjustment).

The Set IRF Defaults button opens the configuration dialog for the IRF defaults which is used to populate the parameters fields in this procedure. These defaults are also used as starting estimates for <irf> non-linear fits, those where the IRF is included in the fitting. When you return from the IRF Defaults procedure, the values for the currently selected response function are updated.

IRF Parameters

These are the parameter values of the IRF selected. These can be individually set when processing multiple data sets as described below. You can manually enter the values, use the spin buttons, or right click for a menu listing the values that would appear in the spin function.

When a value is entered, all of the deconvolutions or convolutions will be automatically updated unless a custom IRF is already present in one or more of the data sets. In such a case you will be presented with an option to perform Full or Partial processing. The Partial option retains the custom deconvolutions or convolutions. A custom setting can occur from either a manual adjustment or a genetic algorithm optimization of a single data set.

Genetic Algorithm Optimization

Genetic Algorithm (GA)

This is an advanced fitting procedure which optimizes the IRF parameters on a per data set basis using a genetic algorithm (GA) designed to find the optimal IRF parameters for that data set. A GA algorithm uses random sampling to navigate local minima or to optimize a procedure where the problem cannot be stated as an equation differentiable with respect to its specific adjustable parameters. In the GA algorithm, the different candidates are spread across simultaneous threads which communicate their progress to one another to hasten convergence. You may thus see very different optimal settings for the GA algorithm with a 4-core (8 hyperthread) CPU as compared to a six, eight, or higher core machine since the convergence mechanism will vary with the core count. The greater the count of cores in your machine, the faster this GA optimization will be. Since all of the available CPU threads are dedicated to this GA algorithm processing of a data set, the optimizations will be sequential, one data set following another. This will look very different from PeakLab's non-linear fitting where all data sets are simultaneously fitted, even the <irf> bearing convolution models.

IRF Deconvolution in Non-Gradient Peaks

In this instance, parameter guesses for the IRF are applied in a Fourier deconvolution procedure and a merit function which seeks to maximize the count and accuracy of baseline points within a specified tolerance is used within the optimization. For every set of estimates tested, a Fourier deconvolution must be made and the merit function evaluated. Even when optimizing a seemingly simple three-parameter (two-component) IRF, there can be tens of thousands of deconvolutions to realize convergence. The GA strategies and algorithm used in PeakLab are fast and efficient, but not immediate. On a typical i7 machine, a 20,000 point data set might require up to ten seconds or so for the default GA fitting.

The GA algorithm works best with bounds on the parameters which confine the estimates to reasonable and mathematically defined values. For this reason, PC Chrom requires that you specify a percent for the allowable variation in a parameter. The defaults assume a three parameter IRF where the first parameter is the system component of the IRF, appreciably varying, the second parameter the exponential instrumental component, likely to vary little, and the third parameter will be the area fraction, likely to also be reasonably well estimated in the defaults. The Parameter 1 % default of 100, the Parameter 2 % default of 20, and the Parameter 3 % of 50 assume IRF defaults which are in the ballpark of the true values. If you specify a % higher than 100%, only the upside range is expanded and the lower bound is constrained to a positive value.

To lock a parameter at a fixed value, simply set the % variation to 0.

For an IRF deconvolution you should only need to use the BsLnZero merit function. You specify a baseline tolerance as a percent. This may need to be adjusted for S/N, increasing this threshold tolerance for baselines with higher noise. For high S/N data, the 0.5% default should be sufficient. Because the GA algorithm depends on an increased measure of stable baseline arising from the deconvolution, and since the IRF deconvolutions add a right-side tailing, only peaks with right-side baseline-resolved decays will factor into the optimization. You will need baseline-resolved peaks to realize accurate IRF deconvolution optimizations using this GA procedure.

Gradient Convolution in HPLC Gradient Peaks

In this instance, for the GA algorithm to be effective, you must specify the desired amplitude attenuation as a fraction of the amplitude of the raw data. For gradient data, a typical value for the AmpAtten for a gradient peak will be 0.86-0.92. If the model is a single parameter model, such as the <g>, there will only be one value of the parameter that produces this amplitude attenuation. If there is a second parameter, as with the <k> model, the GA fit will also seek to maximize the baseline points, the convolution with this attenuation that produces the greatest measure of baseline. Because the GA algorithm with two or more parameter models seeks to find the highest measure of baseline for a given attenuation arising from the convolution, baseline-resolved peaks are needed for an accurate estimation of the gradient model parameters. You may need to zero any small anomalies in the baseline on each side of the peak since these can interfere with the optimization. For this optimization, a single standard peak is recommended.

The two parameter variable order kinetic <k> model will require a greater fitting time. To lock a parameter at a fixed value, such as locking the <k> kinetic order at 0.7, simply set its % variation to 0.

For unwinding the gradient with convolution you should never use the BsLnZero merit function (it is specific to deconvolution). Also, please note that the AmpAtten merit function is only used to optimize the gradient model parameters, and is only applicable to the standard you are using to do this GA parametric estimation. The gradient model parameters, once determined, will not be in any manner tied to the variable attenuation that occurs as a function of the differing peak widths of solutes.

Initiating a Genetic Algorithm Optimization

Click on the Genetic Optimize button to optimize all of the data sets sequentially. When multiple data sets are present, each is given its own independent optimization. All of the buttons in the dialog except the Cancel will be disabled when an optimization is underway. If you cancel the optimization at any point, all of the optimizations thus far completed will be lost. A GA optimized fit will be shown with a different background color in the graphs. This background color will change as the optimizations proceed across multiple data sets.

Using GA Deconvolution Optimization for Tailed Peaks

As discussed in the IRF Estimation 1 topic, intrinsically fronted (-a₃) peaks will be beneficial in fitting convolution models to determine the IRF parameters. In the GenHVL and GenNLC family of models, the a₄ asymmetry adjusts the ZDD, the zero distortion or infinite dilution density, to account the real-world deviation from the theoretical chromatographic shape. Think of a₄ as a subtle adjustment of the primary peak shape. If a peak has a negative a₃, is intrinsically fronted, the impact of a₄ will be mainly in the fronting or the rise of the peak. This is the ideal for fitting a GenHVL<irf> or GenNLC<irf> convolution model to determine the IRF parameters since these mainly impact the observed tailing of a peak.

The problem with fitting <irf> convolution models to sharply tailed peaks is that the a₃ principal distortion will model a tailed peak shape, the a₄ will adjust that tailed envelope, and the two components of an IRF will also model tailed phenomena. For the GenHVL or GenNLC, five parameters will impact the right-side tailing of a strongly tailed peak: a₃ managing the intrinsic chromatographic tailed shape, a₄ modifying the first higher moment of that intrinsic tailing, a₅ managing the 'system' tailing component of the IRF, a₆ mapping the exponential 'instrument' tailing component of the IRF, and a₇ adjusting the area fractions of the two IRF components of the IRF. Understandably, it is close to impossible to get such fits to yield statistically significant estimates for the three parameters of a two component IRF. Indeed, when no IRF is fitted, the intrinsic chromatographic distortion can often 'absorb' much of the IRF tailing, resulting in less accurate peak parameter estimates.

If you are fitting a standard, the addition of an IRF calibrating component that elutes much earlier with intrinsic fronting will solve this problem. A single fronted peak in a standard may be sufficient to bind the shared a₄ ZDD asymmetry to the a₃ fronting so that a₄ does not enter into the IRF tailing. That single intrinsically fronted peak in a multiple component standard will give this determinism to a₄, preventing the fitting problem from being overspecified.

An alternative to the fitting an <irf> convolution model is to use this GA optimization directly on tailed peaks. This should work reasonably well if the S/N is good, and concentrations are not so high as to have an overload state partially present. In the worst case scenario, the optimized GA deconvolution will leave more or less of the asymmetry for a₄ to adjust. You may see a higher variability than you like with a₄, but the primary HVL or NLC a₀-a₃ parameters should be exceptionally stable.

Using GA Deconvolution Optimization for Peaks with Negligible Intrinsic Distortion

When fitting a GenHVL<irf> or GenNLC<irf> model to determine IRF parameters, the best peaks will be from higher concentration standards which have some measure of fronting. The least desirable peaks will be those which have very low a₃ intrinsic distortion values. If the a₃ values are very low, no obvious intrinsic fronting or tailing evident, it will not matter if the peaks are slightly a₃ positive or slightly a₃ negative. The a₄ parameter will statistically detach itself from its function of adjusting the chromatographic shape and this a₄ ZDD correction will instead function to capture a portion of the IRF tailing, rendering the IRF fitted estimates inaccurate.

Also, if a progression of peaks change sign in a₃ with retention time, from intrinsically fronted to intrinsically tailed, it is possible a given peak will elute, even at a significant concentration, near this point of transition, with very little a₃ tailing or fronting.

In these cases, the addition of an IRF calibrating component that elutes much sooner with a fronted shape will be needed if the IRF parameters are to be mapped with the fitting of <irf> convolution model.

If your peaks have very little intrinsic a₃ distortion, you may also be able to use the GA optimization of the deconvolution to get respectable estimates for the IRF. In this case, the optimized GA deconvolution may leave a₄ of subsequent fits widely varying. Again, the a₄ parameter adjusts the primary a₃ chromatographic shape or asymmetry. If the peak has negligible intrinsic distortion (very low magnitude a₃), there is no chromatographic shape for a₄ to act upon. The IRF Deconvolution optimization may produce a high variability in a₄, but it is likely to be of marginal significance anyway, and if it is the primary HVL or NLC a₀-a₃ parameters that you are interested in, these should again be exceptionally stable.

Using GA Convolution Optimization for Gradient Peaks

For gradient HPLC peaks, the IRF will mostly be masked by the gradient. In this case, you are more likely to want to unravel or undo the compression arising from the gradient. In our experience, estimating a gradient model using the generic algorithm is fairly straightforward, especially once you have a clear sense for the amplitude attenuation you expect to see in the solute peak selected for this optimization. It should be a baseline resolved peak from a standard that elutes well into the gradient portion of the elution. Be sure you have selected the Convolve Right option and the AmpAtten merit function for the optimization.

Genetic Algorithm Preferences

Use the Modify Genetic Algorithm Preferences button to set the GA Algorithm controls for the deconvolution optimization.

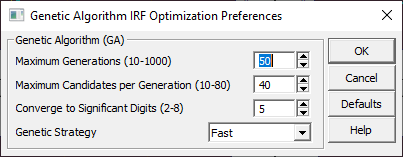
These settings are independent of the GA settings in the Fit Preferences.

The Maximum Generations sets the count of evolutions allowed in the differential evolution GA algorithm. For IRF optimizations to 5 significant digits, the default of 50 should be sufficient. The algorithm concludes at this count of generations if convergence has not yet occurred.

The Maximum Candidates per Generation sets the number of independent random candidates in each generation. The default of 40 appears to work well for IRF optimizations.

The Converge to Significant Digits default of 5 is about what you can realistically expect within a reasonable GA algorithm execution time. If you increase this value, you will also need to increase the Maximum Generations.

There are three Genetic Strategy options from which you can choose. For IRF optimizations, the Fast strategy is recommended. The Random option is slower, but less likely to miss the global minimum in the optimization. The Advanced strategy is used for fitting a large count of parameters in a modeling problem, and should not be needed for the optimization of IRF parameters. If you elect to use other than the Fast strategy, you may need to increase the Maximum Generations since convergence will be slower.

Fourier Filter

Fourier Deconvolution introduces noise in the signal. Unless you have very clean data with very little noise, you will probably wish to use a filter to zero higher frequency or lower dB channels to reduce the noise in the deconvolved signal.

The following Fourier Filter options are available:

None

There is no Fourier filtration performed. This is the setting you will probably want for convolutions which produce their own noise reduction. For deconvolutions, Fourier filtration will generally be beneficial and possibly essential.

Frequency

Specify the actual frequency beyond which all Fourier channels are zeroed. Note that Fourier procedures sometimes use a normalized scale from 0 to 0.5 where 0.5 is the Nyquist frequency. Here you must specify the actual frequency.

dB Norm

Specify the dB threshold below which all Fourier channels are zeroed.

% Channels

Specify the percentage of the channels that will be zeroed. For peak data with a good sampling rate, this value should be quite high. Most of the channels will be zeroed since they contain noise rather than signal.

 
D2 Automatic

This method automatically selects the frequency where the first D2 (second derivative) peak appears after initial drop. Specify the Savitzky-Golay D2 smoothing level as a percent to create this D2 curve. These should be a reasonable measure of latitude. The default SG smoothing widow is 8% of the data range. This method isn't normally viable for deconvolutions, only for general Fourier denoising and convolutions.

Min Automatic

This method automatically selects the minimum in the Fourier spectrum. This is generally where the deconvolution noise increases the magnitude of the signal. Specify the percentage of the initial Fourier channels for this scan. The default band is the initial 20% of the Fourier channels. This method is primarily of value for deconvolutions where the Fourier minimum represents a good estimate of the filter frequency.

For all options, the filter value is set in the adjacent numeric field.

Visually Setting the Fourier Filter Threshold

The Graphically Adjust the Fourier Domain Filter button is used to open the Fourier Filter dialog. This is a Fourier domain filter which can make an immense difference when deconvolving data containing some measure of noise. The power spectrum is displayed as a zero-normalized dB (decibel scale). A change of 20 dB corresponds with one order of magnitude of peak amplitude.

This procedure remains available for convolution, even though any filter setting is ignored. The data shown in this procedure will be the deconvolved data (containing additional noise) or the convolved data (with reduced noise) as opposed to the original data. Use the Fourier Filter procedure available from the Fourier Denoising Data menu option in the main window to inspect the Fourier spectrum of the raw data.

Because of a Gaussian's compact decay, the <g> Gaussian IRF tends to be more difficult to deconvolve (especially as a symmetric IRF in spectroscopic peaks). This Fourier option will allow you to easily see the noise generated and that which must be filtered.

Post-Processing

The Zero Baseline Points checkbox will zero the points in the deconvolution which were seen as baseline in a preceding baseline correction step. Because a Fourier signal must be at zero at both bounds to not introduce bias or 'ringing', a baseline correction step should always precede the Fourier Deconvolution.

The Zero Negative Points checkbox will zero all points post-deconvolution which have a negative value.

Equiv. Noise %

This may be of value with noisy raw data. This will report an estimated Gaussian (white) noise before and after the deconvolution/filtering. With filtering applied, you will probably want to see the output signal with a reduced noise. The % noise in the DC (deconvolved) signal as compared to the incoming is reported below the two Gaussian noise estimates.

Multiple Data Sets

If you have multiple data sets present, all will be shown in this procedure, irrespective of whether or not a data set is selected. The data set selection in the main screen applies only to the View and Compare Data options and the Local Maxima Peaks, Hidden Peaks - Residuals, and the Hidden Peaks - Second Derivative fitting options.

When the OK is selected with all data sets shown, all of the data sets will be preprocessed with the IRF deconvolution or convolution presently shown. Those may include custom processing on one or more of the data sets.

To perform an individual deconvolution on one or more data sets separately, it will be simplest if you double click that graph, or right click and select the Plot This Data Set option from the popup menu. Adjust that specific data set for the deconvolution you wish, including any genetic optimization, and then click OK. The full set of graphs shown will now include this custom processing. A custom deconvolution notification will be given when you exit the procedure when one or more of the data sets were individually processed.

If you wish to select one data set as representative of all of the others, right click this specific graph and select Genetic Algorithm Optimization for this Data Set from the popup menu. This will optimize only this data set. The model and its optimized IRF parameters will then be applied all data sets. If one or more data sets has seen custom processing, you must answer Partial to retain the custom deconvolutions or convolutions. Selecting Full will apply the optimized IRF to all data sets.

Right Click Menu Options

When you right click a graph a popup menu will offer the following options:

Restore Scaling - Undo Zoom

If you have zoomed in the graphs, this option can be used to undo the zoom-in and restore the automatic scaling.

Plot this Data Set

Use this right-click menu option to view or independently process one of the data sets.

Plot All Data Sets

You can use this right-click option to close a local viewing step. You can also close the local viewing by clicking OK-the dialog is restored to where all data sets are shown. You can also double click the graph to restore all data plots.

Choose Color Scheme for Custom Processing...

Use this option to select the color scheme you use to highlight custom convolutions and deconvolutions, including genetic optimizations.

Choose Color Scheme for Non-Custom Processing...

Use this option to select the color scheme to use for the primary (non-custom) convolutions and deconvolutions, those which follow the parameter settings in the dialog.

Genetic Algorithm Optimization for this Data Set

Use this option to initiate a genetic algorithm optimization. If you have multiple data sets and all are presently shown, this option will optimize this specific data set and apply the estimated parameters to all other data sets if Full is subsequently specified, or only those without custom settings if Partial is selected.

PeakLab Graph

All of the graph options are available in the PeakLab graph which is used throughout the program.

Deconvolution Pitfalls

Deconvolution is not without its pitfalls. If you attempt to deconvolve a response function close to the width of a peak or exceeding such, the result is generally nonsense. Even with effective frequency domain noise filtration, noise present at lower frequencies can produce something other than a smooth deconvolution. When the width of the instrument response function is too high, the deconvolved data will sometimes contain negative values or small sinusoidal components.

If a response function width is too small, you essentially have a delta function, a value of 1 in the first value of the array, and all 0's thereafter. Discrete Fourier processing requires some number of channels of non-zero values in the IRF. If you see the inverse disappear completely, the width is probably too small for a discrete data deconvolution. This is why PeakLab's built in <irf> models impose minimum widths.

There are limits to what is possible with deconvolution. For example, it is not possible to use deconvolution to recover a pure spectral line. If you achieve peaks with 30% less width than the original peaks, and the data looks respectable, then you have done well. That is about the extent to which you can hope to "sharpen" peaks using Fourier deconvolution.

Non-Linear Nature of Deconvolution

The nature of convolution and deconvolution is not linear. If a Gaussian is smeared by a symmetric Gaussian IRF, the result is also a Gaussian with a variance equal to the sum of the individual variances. If a Gaussian with SD=3 is convolved with a Gaussian IRF having an equal SD=3, the resulting peak will have a standard deviation of sqrt(3^2+3^2)=4.2. In other words, the price of smearing an equal width peak is not a peak with twice the width, but a peak only 1.4x as wide. In deconvolution, the opposite holds true. That 4.2 SD peak, deconvolved with an SD 3.0 Gaussian, will yield an SD 3.0 Gaussian. In other words, even though you can deconvolve a very large instrument response function, the resulting peak will still have a significant width.

Sequential Sharpening of Spectra

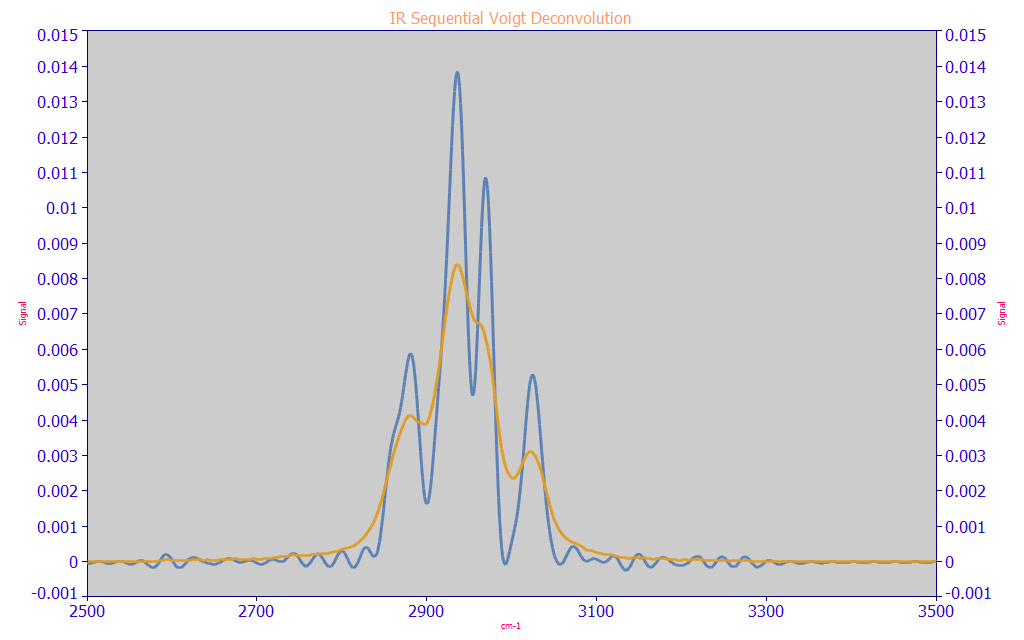
If you want to use Fourier deconvolution to sharpen spectra for visualization purposes, you can sequentially implement Voigt <v> deconvolutions. If you do this, we recommend that you first fit the data to VoigtGL peaks. You will want to share the Gaussian and Lorentzian widths across multiple peaks making up overlapping absorbances. This fit will give you an estimate for the total amount of Gaussian and Lorentzian width available for the deconvolution sharpening. The Lorentzian portion of the <v> Voigt deconvolution (the second IRF parameter) will provide the greatest sharpening, the Gaussian portion of the <v> Voigt deconvolution (the first IRF parameter) will furnish less. What should work reasonably well is to deconvolve about 70% of the two <v> Voigt widths as seen in the peak fit, preserving the same Gaussian-Lorentzian width ratio. Because Lorentzians sum by the widths and Gaussians by the square root of the sum of the variances, 70% of the difference remaining in the widths won't be the equivalent ratio for a second devolution. It may be easiest to fit the data from the first deconvolution and again use 70% of the new fitted widths in a second deconvolution. The following example shows the sharpening of an IR spectrum in a two step deconvolution.